
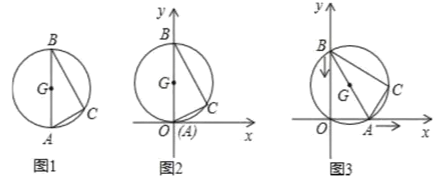
【题目】图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2,现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束,在整个运动过程中,点C运动的路径长是( )
A.![]() πB.2πC.4
πB.2πC.4![]() -2D.10-4
-2D.10-4![]()
【答案】D
【解析】
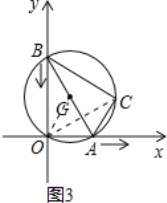
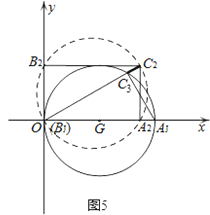
由于在运动过程中,原点O始终在⊙G上,则弧AC的长保持不变,弧AC所对应的圆周角∠AOC保持不变,等于∠XOC,故点C在与x轴夹角为∠ABC的射线上运动.顶点C的运动轨迹应是一条线段,且点C移动到图中C2位置最远,然后又慢慢移动到C3结束,点C经过的路程应是线段C1C2+C2C3.
解:解:如图3,连接OG.
∵∠AOB是直角,G为AB中点,
∴GO=![]() AB=3,
AB=3,
∴原点O始终在⊙G上.
∵∠ACB=90°,AB=6,AC=2,
∴BC=4![]() ,
,
连接OC,则∠AOC=∠ABC,
∴tan∠AOC=![]() ,
,
∴点C在与x轴夹角为∠AOC的射线上运动.
如图4,C1C2=OC2-OC1=6-2=4;
如图5,C2C3=OC2-OC3=6-4![]() ;
;
∴总路径为:C1C2+C2C3=4+6-4![]() =10-4
=10-4![]() .
.
故选:D.



 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
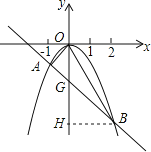
【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),
(1)求二次函数和一次函数解析式.
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′,请你画出△A′B′C′和△A″B″C′,求出![]() 的长?
的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
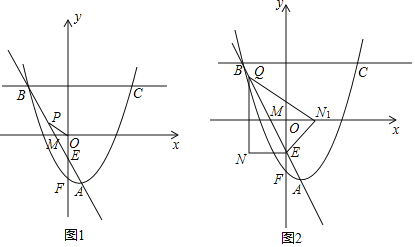
【题目】已知抛物线![]() ,顶点为A,且经过点
,顶点为A,且经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
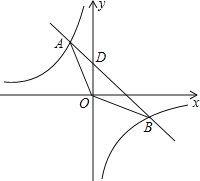
【题目】如图,反比例函数y=﹣![]() 与一次函数y=﹣x+2的图象交于A、B两点.
与一次函数y=﹣x+2的图象交于A、B两点.
(1)试求A、B两点的坐标;
(2)直线AB交y轴于点C,求tan∠AOC的值;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论错误的是( )
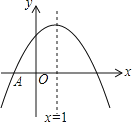
A.3a+b<0B.﹣2≤a≤﹣lC.abc>0D.9a+3b+2c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
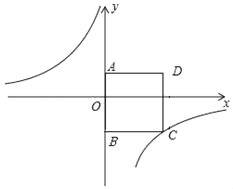
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为(0,3),点B的坐标为(0,﹣4),反比例﹣函数y=![]() (k≠0)的图象经过点C.
(k≠0)的图象经过点C.
(1)求反比例函数的解析式;
(2)点P是反比例函数在第二象限的图象上的一点,若△PBC的面积等于正方形ABCD的面积,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com