
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1) 求证:AF=DC;
(2) 若AC⊥AB,试判断四边形ADCF的形状,并说明理由;
(3) 当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
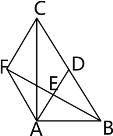
【答案】(1)证明见解析(2)四边形ADCF是菱形(3)当AB=AC且∠BAC=90°时,四边形ADCF是正方形
【解析】
(1)连接DF,由AAS证明△AFE≌△DBE,得出AF=BD,即可得出答案;
(2)根据平行四边形的判定得出平行四边形ADCF,求出AD=CD,根据菱形的判定得出即可;
(3)根据等腰三角形性质求出AD⊥BC,得出∠ADC=90°,根据正方形的判定得出即可.
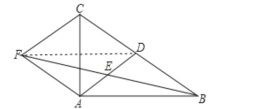
(1)证明:连接DF,
∵E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AFE和△DBE中,
∠AFE=∠DBE,∠FEA=∠DEB,AE=DE,
∴△AFE≌△DBE(AAS),
∴EF=BE,
∵AE=DE,
∴四边形AFDB是平行四边形,
∴BD=AF,
∵AD为中线,
∴DC=BD,
∴AF=DC;
(2)四边形ADCF的形状是菱形,理由如下:
∵AF=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,
∴∠CAB=90°,
∵AD为中线,
∴AD=![]() BC=DC,
BC=DC,
∴平行四边形ADCF是菱形;
(3)当△ABC满足AC=AB且∠BAC=90°时,四边形ADCF为正方形,理由如下:
∵∠CAB=90°,AC=AB,AD为中线,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ADCF是菱形,
∴四边形ADCF是正方形.


科目:初中数学 来源: 题型:
【题目】在干燥的路面上,使车子停止前进所需的刹车距离s(m)与车速v(km/h)的关系是s=![]() v+
v+![]() v2 .
v2 .
(1)当v分别是48,64时,求相应的刹车距离s的值;
(2)司机小李正以72km/h的速度行驶,突然发现前方大约60m处有一不明障碍物,他立即刹车,车会撞上障碍物吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
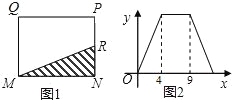
【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y=![]() 时,x=10
时,x=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8, AC=10,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,连接GD,若∠EFC=60°,则EG的长为( )

A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式.例如,分式是![]() ,
,![]() 是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式
是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式![]() ,
,![]() 是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,
是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,![]() =
=![]() =1-
=1-![]() .
.
(1)将假分式![]() 化为一个整式与一个真分式的和;
化为一个整式与一个真分式的和;
(2)如果分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,有下列说法:①点
,有下列说法:①点![]() 与点
与点![]() 的距离是线段
的距离是线段![]() 的长;②点
的长;②点![]() 到直线
到直线![]() 的距离是线段
的距离是线段![]() 的长;③线段
的长;③线段![]() 是
是![]() 边
边![]() 上的高;④线段
上的高;④线段![]() 是
是![]() 边
边![]() 上的高.
上的高.
上述说法中,正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
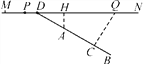
【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音(XRS)的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com