练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．下列各式中，不论字母取何值时分式都有意义的是（　　）
    A．$\frac{1}{2x+1}$B．$\frac{1}{2x-1}$C．$\frac{1-3x}{{x}^{2}}$D．$\frac{5x+3}{2{x}^{2}+1}$

    分析 根据分式有意义的条件是分母不等于零列出不等式，可得答案．

    解答 解：∵2x2+1＞1，
    ∴不论字母取何值$\frac{5x+3}{2{x}^{2}+1}$都有意义，
    故选：D．

    点评 本题考查的是分式有意义的条件，掌握分式有意义的条件是分母不等于零是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．已知a-b=2，a2-ab-c2+2c=0，点P（x1，y1），Q（x2，y2）在反比例函数y=$\frac{a}{x}$（a≠0）图象上，且满足x2-x1=8，$\frac{1}{{y}_{2}}$-$\frac{1}{{y}_{1}}$＞2，求整数c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

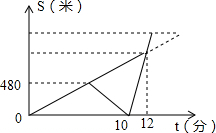    10．小明和哥哥以每分钟80米的速度从家出发步行去爷爷家．在途中，哥哥发现忘记带给爷爷买的礼物，于是小明继续前行，哥哥以每分钟120米的速度沿原路跑回家，然后乘出租车赶往爷爷家，途中追上小明后，带上他一同乘车到爷爷家，结果到爷爷家的时间比预计步行的时间早了3分钟（其中回家取东西、上下车时间忽略不计）．如图反映了小明和哥哥离家距离与时间之间的关系．
    （1）小明和哥哥离开家6分钟时，哥哥发现忘记带礼物；
    （2）求出图中出租车行驶路程s与时间t的函数关系式（不必写出t的取值范围）；
    （3）请直接写出小明家到爷爷家的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：-12+（1-$\sqrt{3}$）2+|-2015|+2sin30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，点D在AC的垂直平分线上，AB∥CD，若∠ADC=130°，则∠BAC的度数是25°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．先化简，再求值：$\frac{a-2}{{{a^2}-1}}÷（{a-1-\frac{2a-1}{a+1}}）$，其中a为不等式组$\left\{\begin{array}{l}{3x-2＞7}\\{\frac{2x+1}{3}≥x-1}\end{array}\right.$的正整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

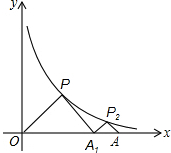    11．如图，△POA1、△P2A1A都是等腰直角三角形，直角顶点P、P2在函数y=$\frac{4}{x}$（x＞0）的图象上，斜边OA1、A1A都在x轴上，则点A的坐标是（　　）
    A．（4，0）B．（4$\sqrt{2}$，0）C．（2，0）D．（2$\sqrt{2}$，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

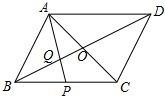    8．如图，在?ABCD中，对角线AC，BD相交于点O，P是BC边中点，AP交BD于点Q．则$\frac{OQ}{OB}$的值为$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

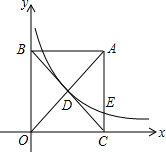    9．如图，已知矩形ABOC的对角线相交于点D，O为坐标原点，OC在x轴的正半轴上，双曲线y=$\frac{k}{x}$（k＞0）经过点D，与边AC相交于点E．若OC2=CE•CA，则直线OA的解析式为y=2x．

    查看答案和解析>>

    同步练习册答案