
【题目】已知∠AOC与∠BOD具有公共顶点,∠COD是两个角叠合的部分.
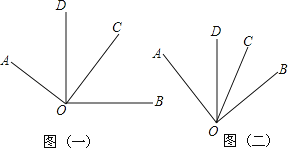
(1)若∠AOC=∠BOD=90°,观察图形(一)并完成下列问题:
①直接写出图中两个相等的锐角: = ;
②如果∠COD=40°,则∠AOB= ,若∠AOB=150°,则∠COD= ;
③猜想∠AOB+∠DOC= °,请说明理由.
(2)探究图形(二):若∠AOC=60°,∠BOD=50°,则∠AOB+∠DOC= °,请说明理由.
【答案】(1)①∠AOD,∠BOC;②140°,30°;③180°,理由见解析;(2)110°,理由见解析
【解析】
(1)①利用同角的余角相等得出答案即可;
②③利用余角的意义和角的和差计算即可;
(2)利用角的和与差计算即可.
解:(1)①若∠AOC=∠BOD=90°,
∠AOD+∠COD=∠BOC+∠COD=90°,
∴∠AOD=∠BOC;
②∵∠COD=40°,
∴∠AOD=50°,
∠AOB=∠AOD+∠BOD=140°;
若∠AOB=150°,则∠AOD=∠AOB﹣90°=60°,
∴∠COD=90°﹣∠AOD=30°.
③∠AOB+∠DOC=180°,
理由:∠AOB+∠DOC=90°+∠AOD+∠DOC=90°+90°=180°;
(2)∠AOB+∠DOC=110°,
理由:若∠AOC=60°,∠BOD=50°,
则∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠BOD=110°.


科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
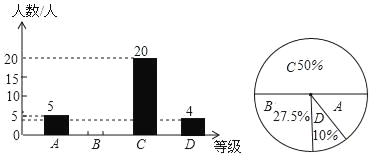
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
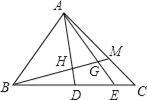
A. 3:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B是线段AC上一点,AC=4AB,AB=6cm,直线MN经过线段BC的中点P.
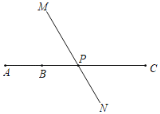
(1)图中共有线段_____条,图中共有射线_____条.
(2)图中与∠MPC互补的角是_____.
(3)线段AP的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() ,
,![]() 上,连接
上,连接![]() .
.
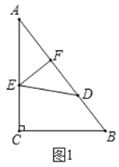
(1)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,如图1,若
处,如图1,若![]() ,求
,求![]() 的长;
的长;
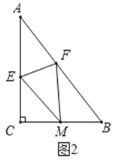
(2)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,如图2,若
处,如图2,若![]() .
.
①求![]() 的长;
的长;
②求四边形![]() 的面积;
的面积;
(3)若点![]() 在射线
在射线![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 关于
关于![]() 所在直线的对称点为点
所在直线的对称点为点![]() ,问:是否存在以
,问:是否存在以![]() 、
、![]() 为对边的平行四边形,若存在,求出
为对边的平行四边形,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B 村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每100km耗油3升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
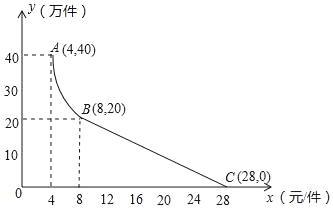
【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某纺织厂收购某种特色棉花,若直接转卖这种特色棉花,则每吨可获得的利润为500元.若经过![]() 级加工再转卖,则每吨可获得的利润为1000元;若经过
级加工再转卖,则每吨可获得的利润为1000元;若经过![]() 级加工再转卖,则每吨可获得的利润为2000元.已知该纺织厂对棉花进行
级加工再转卖,则每吨可获得的利润为2000元.已知该纺织厂对棉花进行![]() 级加工,每天可加工16吨;进行
级加工,每天可加工16吨;进行![]() 级加工,每天可加工6吨,且这两种等级的加工不能同时进行.若该纺织厂收购了140吨这种特色棉花,决定15天内加工完,且有如下三种可行方案:
级加工,每天可加工6吨,且这两种等级的加工不能同时进行.若该纺织厂收购了140吨这种特色棉花,决定15天内加工完,且有如下三种可行方案:
方案一:将所收购的特色棉花直接转卖.
方案二:将尽可能多的特色棉花进行![]() 级加工,余下的部分直接转卖.
级加工,余下的部分直接转卖.
方案三:一部分进行![]() 级加工,另一部分进行
级加工,另一部分进行![]() 级加工,恰好15天完成.
级加工,恰好15天完成.
若你是该纺织厂负责人,想要获利最多,你决定使用哪套方案?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com