练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，扇形OMN与正方形ABCD，半径OM与边AB重合，弧MN的长等于AB的长，已知AB=2，扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止，则点O经过的路径长 ．

    【答案】2+4π
    【解析】解：当扇形绕B旋转时，路径长是 =2π，

    当弧NM在BC上时，O经过的路径长是2；

    当扇形绕C旋转时，路径长是 =2π；

    则点O经过的路径长2+2π+2π=2+4π．

    故答案是：2+4π．

    【考点精析】掌握弧长计算公式是解答本题的根本，需要知道若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(一)问题提出：如何把n个边长为1的正方形，剪拼成一个大正方形？

    (二)解决方法

    探究一：若n是完全平方数，我们不用剪切小正方形，可直接将小正方形拼成一个大正方形，如图(1)，用四个边长为1的小正方形可以拼成一个大正方形．

    问题1：请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形．

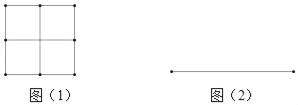
    探究二：若n＝2，5，10，13等这些数，都可以用两个正整数的平方和来表示，以n＝5为例，用5个边长为1的小正方形剪拼成一个大正方形．

    (1)计算：拼成的大正方形的面积为5，边长为，可表示成；

    (2)剪切：如图(3)将5个小正方形按如图所示分成5部分，虚线为剪切线；

    (3)拼图：以图(3)中的虚线为边，拼成一个边长为的大正方形，如图(4)．

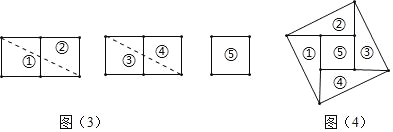
    问题2：请仿照上面的研究方式，用13个边长为1的小正方形剪拼成一个大正方形；

    (1)计算：拼成的大正方形的面积为____，边长为_____，可表示成____；

    (2)剪切：请仿照图(3)的方法，在图(5)的位置画出图形．

    (3)拼图：请仿照图(4)的方法，在图(6)的位置出拼成的图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB＝6，AD＝8，P是AD上的动点，PE⊥AC，PF⊥BD于F，求PE+PF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1=∠2，∠5=∠6，∠3=∠4，试说明AE∥BD，AD∥BC．请完成下列证明过程．

    证明：

    ∵∠5=∠6，

    ∴AB∥CE(　　)，

    ∴∠3=__________

    ∵∠3=∠4，

    ∴∠4=∠BDC(　　)，

    ∴　　　　∥BD(　　)，

    ∴∠2=　　　　(　　)

    ∵∠1=∠2，

    ∴∠1=______，

    ∴AD∥BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=3，BC=5，以B为圆心BC为半径画弧交AD于点E，连接CE，作BF⊥CE，垂足为F，则tan∠FBC的值为（ ）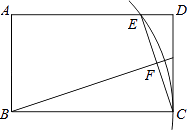

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】市场上的红茶由茶原液与纯净水按一定比例配制而成，其中购买一吨茶原液的钱可以买15 吨纯净水。由于今年以来茶产地连续大旱，茶原液收购价上涨50%．纯净水价也上涨了10%，导致配制的这种茶饮料成本上涨40%，问这种茶饮料中茶原液与纯净水的配制比例为_______ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，给出下列四个条件：① ∠BAC=∠DCA；② ∠DAC=∠BCA；③ ∠ABD=∠CDB；④ ∠ADB=∠CBD，其中能使 AD∥BC的条件是（ ）

    A.①②B.③④C.②④D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，ABCD是边长为60cm的正方形硬纸片，切去四个全等的等腰直角三角形（阴影部分所示），其中E，F在AB上；再沿虚线折起，点A，B，C，D恰好重合于点O处（如图②所示），形成有一个底面为正方形GHMN的包装盒，设AE=x （cm）．

    （1）求线段GF的长；（用含x的代数式表示）
    （2）当x为何值时，矩形GHPF的面积S （cm2）最大？最大面积为多少？
    （3）试问：此种包装盒能否放下一个底面半径为15cm，高为10cm的圆柱形工艺品，且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内？若能，请求出满足条件的x的值或范围；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解全校学生对新闻，体育．动画、娱乐、戏曲五类电视节目的喜爱情况，机调查了100名学生，结果如扇形图所示，依据图中信息，回答下列问题： （1）在被调查的学生中，喜欢“动画”节目的学生有 _____（名）； （2）在扇形统计图中，喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 _____（度）．

    查看答案和解析>>

    同步练习册答案