
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:随机抽取甲乙两所学校的名学生的数学成绩进行
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述数据:按如下数据段整理、描述这两组数据,分析数据:
分段 学校 |
|
|
|
|
|
|
|
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 |
| 91 | 268.43 |
乙 | 81.95 | 86 | 88 | 115.25 |
(1)经统计,表格中![]() 的值是__________.
的值是__________.
(2)得出结论
①若甲学校有600名初二学生,估计这次考试成绩80分以上人数为__________.
②可以推断出__________学校学生的数学水平较高,理由为:__________.(至少从两个不同的角度说明推断的合理性)
【答案】(1)88;(2)①450,②甲,甲的中位数及众数均高于乙校,说明甲校学生的数学水平较高
【解析】
(1)先整理统计表,得到总人数是20人,取中间两个数的平均数即可得到m;
(2)①用样本中80分以上的人数除以样本总人数再乘以全校的人数600即可得到答案;
②根据统计表分析即可得到答案,答案不唯一.
解:整理、描述数据
分段 学校 |
|
|
|
|
|
|
|
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 4 | 2 | 8 | 5 |
分析数据
(1)经统计表格,得到总人数=1+1+0+0+3+7+8=20(人),
中间两个数据都是88,
∴![]() 的值是88.
的值是88.
故答案为:88;
(2)①甲学校600名初二学生在这次考试成绩80分以上人数为![]() (人)
(人)
故答案为:450.
②答案不唯一,理由须支撑推断结论.
答案为:甲,甲的中位数及众数均高于乙校,说明甲校学生的数学水平较高.


科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:


(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的 概率是![]() ;中再放进1个黑球,这时取得黑球的概率变为
;中再放进1个黑球,这时取得黑球的概率变为![]()
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y个白球进行摸球游戏。约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
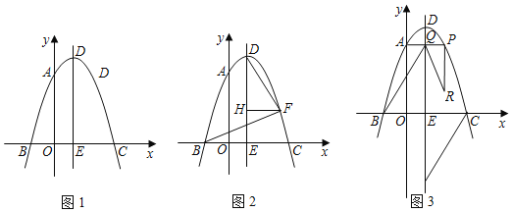
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=﹣x2+2mx+3m2与x轴相交于点B、C(点B在点C的左侧),与y轴相交于点A,点D为抛物线的顶点,抛物线的对称轴交x轴于点E.
(1)如图1,当AO+BC=7时,求抛物线的解析式;
(2)如图2,点F是抛物线的对称轴右侧一点,连接BF、CF、DF,过点F作FH∥x轴交DE于点H,当∠BFC=∠DFB+∠BFH=90°时,求点H的纵坐标;
(3)如图3,在(1)的条件下,点P是抛物线上一点,点P、点A关于直线DE对称,点Q在线段AP上,过点P作PR⊥AP,连接BQ、QR,满足QB平分∠AQR,tan∠QRP=![]() ,点K在抛物线的对称轴上且在x轴下方,当CK=BQ时,求线段DK的长.
,点K在抛物线的对称轴上且在x轴下方,当CK=BQ时,求线段DK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.
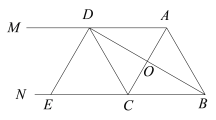
(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
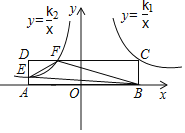
【题目】如图,矩形ABCD的顶点A,B在x轴上,且关于y轴对称,反比例函数y=![]() (x>0)的图象经过点C,反比例函数y=
(x>0)的图象经过点C,反比例函数y=![]() (x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
(x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·泰安)如图,是将抛物线![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,另一交点为
,另一交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.

(1)求抛物线的函数表达式;
(2)若点![]() 为抛物线上一点,且
为抛物线上一点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 是抛物线上一点,点
是抛物线上一点,点![]() 是一次函数
是一次函数![]() 的图象上一点,若四边形
的图象上一点,若四边形![]() 为平行四边形,这样的点
为平行四边形,这样的点![]() 是否存在?若存在,分别求出点
是否存在?若存在,分别求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
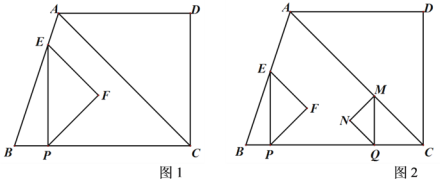
【题目】如图1,△ABC中,AC=![]() ,∠ACB=45°,tanB=3,过点A作BC的平行线,与过C且垂直于BC的直线交于点D,一个动点P从B出发,以每秒1个单位长度的速度沿BC方向运动,过点P作PE⊥BC,交折线BA-AD于点E,以PE为斜边向右作等腰直角三角形PEF,设点P的运动时间为t秒(t>0).
,∠ACB=45°,tanB=3,过点A作BC的平行线,与过C且垂直于BC的直线交于点D,一个动点P从B出发,以每秒1个单位长度的速度沿BC方向运动,过点P作PE⊥BC,交折线BA-AD于点E,以PE为斜边向右作等腰直角三角形PEF,设点P的运动时间为t秒(t>0).
(1)当点F恰好落在CD上时,此时t的值为 ;
(2)若P与C重合时运动结束,在整个运动过程中,设等腰直角三角形PEF与四边形ABCD重叠部分的面积为S,请求出S与t之间的函数关系式,并写出自变量t的取值范围;
(3)如图2,在点P开始运动时,BC上另一点Q同时从点C出发,以每秒2个单位长度沿CB方向运动,当Q到达B点时停止运动,同时点P也停止运动,过Q作QM⊥BC交射线CA于点M,以QM为斜边向左作等腰直角三角形QMN,若点P运动到t秒时,两个等腰直角三角形分别有一条边恰好落在同一直线上,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=﹣![]() (x<0)的图象交于C,D两点,点C的横坐标为﹣1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法正确的是( )
(x<0)的图象交于C,D两点,点C的横坐标为﹣1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法正确的是( )
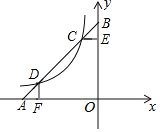
A.b=5
B.BC=AD
C.五边形CDFOE的面积为35
D.当x<﹣2时,y1>y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com