
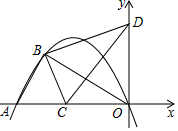
 如图,抛物线y=$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$与x轴交于点A和原点O,点B(-8,n)在抛物线上,连接AB、OB.
如图,抛物线y=$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$与x轴交于点A和原点O,点B(-8,n)在抛物线上,连接AB、OB.分析 (1)通过解方程$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$=0可得A点坐标,从而得到OA的长;然后把B(-8,n)代入y=$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$可求出n的值;
(2)设D(0,t),利用勾股定理得到(m+8)2+42+82+(t-4)2=m2+t2,则可用m表示t,即t=2m+10,所以D(0,2m+10),然后根据三角形面积公式,利用S△BCD=S△OBD+S△BCD-S△OCD可得到S=m2+16m+80,再利用二次函数的性质解决问题;
(3)先利用勾股定理的逆定理证明△AOB为直角三角形,∠ABO=90°,则∠COD=∠ABO,然后根据相似三角形的判定方法,当$\frac{OC}{AB}$=$\frac{OD}{BO}$时,△OCD∽△BAO或当$\frac{OC}{OB}$=$\frac{OD}{BA}$时,△OCD∽△BOA,于是利用相似比得到关于m的方程,则解方程可确定满足条件的m的值.
解答 解:(1)当y=0时,$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$=0,解得x1=0,x2=10,则A(-10,0),
所以OA=10,
把B(-8,n)代入y=$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$得n=-$\frac{1}{4}$×64+$\frac{5}{2}$×8=4;
故答案为4,10;
(2)设D(0,t),
∵BC2+BD2=CD2,
∴(m+8)2+42+82+(t-4)2=m2+t2,
∴t=2m+10,
即D(0,2m+10),
∵S△BCD=S△OBD+S△BCD-S△OCD,
∴S=$\frac{1}{2}$•(2m+10)•8+$\frac{1}{2}$•(-m)•4-$\frac{1}{2}$•(-m)•(2m+20)
=m2+16m+80
=(m+8)2+16,
当m=-8时,S有最大值,最大值为16;
(3)存在.
∵OA2=100,AB2=(-8+10)2+42=20,OB2=82+42=80,
∴AB2+OB2=OA2,
∴△AOB为直角三角形,∠ABO=90°,
∵∠COD=∠ABO,
∴当$\frac{OC}{AB}$=$\frac{OD}{BO}$时,△OCD∽△BAO,
即$\frac{-m}{2\sqrt{5}}$=$\frac{2m+20}{4\sqrt{5}}$,解得m=-5;
当$\frac{OC}{OB}$=$\frac{OD}{BA}$时,△OCD∽△BOA,
即$\frac{-m}{4\sqrt{5}}$=$\frac{2m+20}{2\sqrt{5}}$,解得m=-8,
综上所述,m的值为-8或-5时,△OCD与△OAB相似.
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质和相似三角形的判定方法;会利用待定系数法求函数解析式;学会用勾股定理的逆定理证明直角三角形;理解坐标与图形性质,记住两点间的距离公式;会利用分类讨论的思想解决数学问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )
如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )| A. | 22 | B. | 36 | C. | 46 | D. | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com