
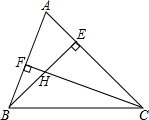
 如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.
如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度. 分析 先根据三角形内角和定理计算出∠A=180°-∠ABC-∠ACB=62°,再根据高的定义得∠AEB=∠AFC=90°,于是利用四边形内角和为360°可计算出∠EHF=118°,然后根据对顶角相等得到∠BHC的度数.
解答 解:∵∠ABC=65°,∠ACB=45°,
∴∠A=180°-∠ABC-∠ACB=70°,
∵BE、CF是两边AC、AB上的高,
∴∠AEB=∠AFC=90°,
而∠A+∠AFH+∠AEH+∠EHF=360°,
∴∠EHF=180°-70°=110°,
∴∠BHC=110°.
点评 本题考查了三角形内角和定理:三角形内角和是180°,高的定义,以及四边形内角和为360°,注意角的运算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:
如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),
已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 选手 | 演讲内容 | 演讲能力 | 演讲效果 |
| 甲 | 85 | 95 | 95 |
| 乙 | 95 | 85 | 95 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com