
”¾ĢāÄæ”æČēĶ¼1£¬¶ž“ĪŗÆŹży£½ax2©2ax©3a£Øa£¼0£©µÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄÓŅ²ą£©£¬ÓėyÖįµÄÕż°ėÖį½»ÓŚµćC£¬¶„µćĪŖD£®
£Ø1£©Ē󶄵ćDµÄ×ų±ź£ØÓĆŗ¬aµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©ČōŅŌADĪŖÖ±¾¶µÄŌ²¾¹żµćC£®
¢ŁĒóÅ×ĪļĻßµÄŗÆŹż¹ŲĻµŹ½£»
¢ŚČēĶ¼2£¬µćEŹĒyÖįøŗ°ėÖįÉĻŅ»µć£¬Į¬½ÓBE£¬½«”÷OBEČĘĘ½ĆęÄŚÄ³Ņ»µćŠż×Ŗ180”ć£¬µĆµ½”÷PMN£ØµćP”¢M”¢N·Ö±šŗĶµćO”¢B”¢E¶ŌÓ¦£©£¬²¢ĒŅµćM”¢N¶¼ŌŚÅ×ĪļĻßÉĻ£¬×÷MF”ĶxÖįÓŚµćF£¬ČōĻ߶ĪMF£ŗBF£½1£ŗ2£¬ĒóµćM”¢NµÄ×ų±ź£»
¢ŪµćQŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬ŅŌQĪŖŌ²ŠÄµÄŌ²¹żA”¢BĮ½µć£¬²¢ĒŅŗĶÖ±ĻßCDĻąĒŠ£¬ČēĶ¼3£¬ĒóµćQµÄ×ų±ź£®

”¾“š°ø”æ£Ø1£©£Ø1£¬©4a£©£»£Ø2£©¢Ły=©x2+2x+3£»¢ŚM£Ø![]() £¬
£¬![]() £©”¢N£Ø
£©”¢N£Ø![]() £¬
£¬![]() £©£»¢ŪµćQµÄ×ų±źĪŖ£Ø1£¬©4+2
£©£»¢ŪµćQµÄ×ų±źĪŖ£Ø1£¬©4+2![]() £©»ņ£Ø1£¬©4©2
£©»ņ£Ø1£¬©4©2![]() £©£®
£©£®
”¾½āĪö”æ
·ÖĪö: £Ø1£©½«¶ž“ĪŗÆŹżµÄ½āĪöŹ½½ųŠŠÅä·½¼“æɵƵ½¶„µćDµÄ×ų±ź£®
£Ø2£©¢ŁŅŌADĪŖÖ±¾¶µÄŌ²¾¹żµćC£¬¼“µćCŌŚŅŌADĪŖÖ±¾¶µÄŌ²µÄŌ²ÖÜÉĻ£¬ŅĄ¾ŻŌ²ÖܽĒ¶ØĄķ²»ÄŃµĆ³ö”÷ACDŹĒøöÖ±½ĒČż½ĒŠĪ£¬ĒŅ”ĻACD£½90”ć£¬Aµć×ų±źæÉµĆ£¬¶ųC”¢DµÄ×ų±źæÉÓÉa±ķ“ļ³öĄ“£¬ŌŚµĆ³öAC”¢CD”¢ADµÄ³¤¶Č±ķ“ļŹ½ŗó£¬ŅĄ¾Ż¹“¹É¶ØĄķĮŠµČŹ½¼“æÉĒó³öaµÄÖµ£®
¢Ś½«”÷OBEČĘĘ½ĆęÄŚÄ³Ņ»µćŠż×Ŗ180”ćµĆµ½”÷PMN£¬ĖµĆ÷ĮĖPMÕżŗĆŗĶxÖįĘ½ŠŠ£¬ĒŅPM£½OB£½1£¬ĖłŅŌĒóM”¢NµÄ×ų±ź¹Ų¼üŹĒĒó³öµćMµÄ×ų±ź£»Ź×ĻČøł¾Ż¢ŁµÄŗÆŹż½āĪöŹ½Éč³öMµćµÄ×ų±ź£¬Č»ŗóøł¾ŻĢāøÉĢõ¼ž£ŗBF£½2MF×÷ĪŖµČĮæ¹ŲĻµ½ųŠŠ½ā“š¼“æÉ£®
¢ŪÉč”ŃQÓėÖ±ĻßCDµÄĒŠµćĪŖG£¬Į¬½ÓQG£¬ÓÉC”¢DĮ½µćµÄ×ų±ź²»ÄŃÅŠ¶Ļ³ö”ĻCDQ£½45”ć£¬ÄĒĆ“”÷QGDĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬¼“QD £½2QG £½2QB £¬Éč³öµćQµÄ×ų±ź£¬Č»ŗóÓĆQµćׯ×ų±ź±ķ“ļ³öQD”¢QBµÄ³¤£¬øł¾ŻÉĻĆęµÄµČŹ½ĮŠ·½³Ģ¼“æÉĒó³öµćQµÄ×ų±ź£®
Ļź½ā:
£Ø1£©”ßy=ax2©2ax©3a=a£Øx©1£©2©4a£¬
”ąD£Ø1£¬©4a£©£®
£Ø2£©¢Ł”ßŅŌADĪŖÖ±¾¶µÄŌ²¾¹żµćC£¬
”ą”÷ACDĪŖÖ±½ĒČż½ĒŠĪ£¬ĒŅ”ĻACD=90”ć£»
ÓÉy=ax2©2ax©3a=a£Øx©3£©£Øx+1£©ÖŖ£¬A£Ø3£¬0£©”¢B£Ø©1£¬0£©”¢C£Ø0£¬©3a£©£¬Ōņ£ŗ
AC2=9a2+9ӢCD2=a2+1ӢAD2=16a2+4
Óɹ“¹É¶ØĄķµĆ£ŗAC2+CD2=AD2£¬¼“£ŗ9a2+9+a2+1=16a2+4£¬
»Æ¼ņ£¬µĆ£ŗa2=1£¬ÓÉa£¼0£¬µĆ£ŗa=©1£¬
¢Ś”ßa=©1£¬
”ąÅ×ĪļĻߵĽāĪöŹ½£ŗy=©x2+2x+3£¬D£Ø1£¬4£©£®
”ß½«”÷OBEČĘĘ½ĆęÄŚÄ³Ņ»µćŠż×Ŗ180”ćµĆµ½”÷PMN£¬
”ąPM”ĪxÖį£¬ĒŅPM=OB=1£»
ÉčM£Øx£¬©x2+2x+3£©£¬ŌņOF=x£¬MF=©x2+2x+3£¬BF=OF+OB=x+1£»
”ßBF=2MF£¬
”ąx+1=2£Ø©x2+2x+3£©£¬»Æ¼ņ£¬µĆ£ŗ2x2©3x©5=0
½āµĆ£ŗx1=©1£ØÉįČ„£©”¢x2=![]() .
.
”ąM£Ø![]() £¬
£¬![]() £©”¢N£Ø
£©”¢N£Ø![]() £¬
£¬![]() £©£®
£©£®
¢ŪÉč”ŃQÓėÖ±ĻßCDµÄĒŠµćĪŖG£¬Į¬½ÓQG£¬¹żC×÷CH”ĶQDÓŚH£¬ČēĻĀĶ¼£ŗ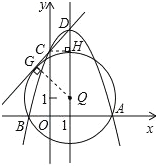
”ßC£Ø0£¬3£©”¢D£Ø1£¬4£©£¬
”ąCH=DH=1£¬¼“”÷CHDŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”÷QGDŅ²ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬¼“£ŗQD2=2QG2£»
ÉčQ£Ø1£¬b£©£¬ŌņQD=4©b£¬QG2=QB2=b2+4£»
µĆ£ŗ£Ø4©b£©2=2£Øb2+4£©£¬
»Æ¼ņ£¬µĆ£ŗb2+8b©8=0£¬½āµĆ£ŗb=©4”Ą2![]() £»
£»
¼“µćQµÄ×ų±źĪŖ£Ø1£¬![]() £©»ņ£Ø1£¬
£©»ņ£Ø1£¬![]() £©£®
£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬AB=AC£¬”ĻA=36”ć£¬ACµÄ“¹Ö±Ę½·ÖĻß½»ABÓŚE£¬DĪŖ“¹×ć£¬Į¬½įEC£®
£Ø1£©Ēó”ĻECDµÄ¶ČŹż.
£Ø2£©ČōCE=9£¬ĒóBCµÄ³¤.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷ѧĻ°µēѧÖŖŹ¶ŗó£¬ÓĆĖÄøöæŖ¹Ų°“¼ü£ØĆæøöæŖ¹Ų°“¼ü±ÕŗĻµÄæÉÄÜŠŌĻąµČ£©”¢Ņ»øöµēŌ“ŗĶŅ»øöµĘÅŻÉč¼ĘĮĖŅ»øöµēĀ·Ķ¼
£Ø1£©ČōŠ”Ć÷Éč¼ĘµÄµēĀ·Ķ¼ČēĶ¼1£ØĖÄøöæŖ¹Ų°“¼ü¶¼“¦ÓŚ“ņæŖדĢ¬£©ČēĶ¼ĖłŹ¾£¬ĒóČĪŅā±ÕŗĻŅ»øöæŖ¹Ų°“¼ü£¬µĘÅŻÄÜ·¢¹āµÄøÅĀŹ£»

£Ø2£©ČōŠ”Ć÷Éč¼ĘµÄµēĀ·Ķ¼ČēĶ¼2£ØĖÄøöæŖ¹Ų°“¼ü¶¼“¦ÓŚ“ņæŖדĢ¬£©ČēĶ¼ĖłŹ¾£¬ĒóĶ¬Ź±Ź±±ÕŗĻĘäÖŠµÄĮ½øöæŖ¹Ų°“¼ü£¬µĘÅŻÄÜ·¢¹āµÄøÅĀŹ£®£ØÓĆĮŠ±ķ»ņŹ÷דĶ¼·Ø£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
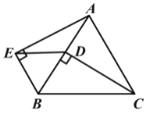
”¾ĢāÄæ”æČēĶ¼,”÷ABCŹĒµČ±ßČż½ĒŠĪ,CD”ĶABÓŚµćD,”ĻAEB=90”ć,CD=AE.
ĒóÖ¤:(1)”÷BCD”Õ”÷BAE;(2)”÷EBDŹĒµČ±ßČż½ĒŠĪ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬PĪŖµČ±ß”÷ABCĶāŅ»µć£¬AH“¹Ö±Ę½·ÖPCÓŚµćH£¬”ĻBAPµÄĘ½·ÖĻß½»PCÓŚµćD£®

£Ø1£©ĒóÖ¤£ŗDP£½DB£»
£Ø2£©ĒóÖ¤£ŗDA+DB£½DC£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬”ĻB=60”ć£¬¶Ō½ĒĻßACĘ½·Ö½Ē”ĻBAD£¬µćPŹĒ”÷ABCÄŚŅ»µć£¬Į¬½ÓPA”¢PB”¢PC£¬ČōPA=6£¬PB=8£¬PC=10£¬ŌņĮāŠĪABCDµÄĆ껿µČÓŚ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC£½90”ć£¬ADŹĒøߣ¬BEŹĒÖŠĻߣ¬CFŹĒ½ĒĘ½·ÖĻߣ¬CF½»ADÓŚG£¬½»BEÓŚH£®ĻĀĮŠ½įĀŪ£ŗ¢ŁS”÷ABE£½S”÷BCE£»¢Ś”ĻAFG£½”ĻAGF£»¢Ū”ĻFAG£½2”ĻACF£»¢ÜBH£½CH£®ĘäÖŠĖłÓŠÕżČ·½įĀŪµÄŠņŗÅŹĒ
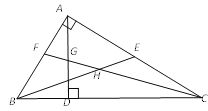
A.¢Ł¢Ś¢Ū¢ÜB.¢Ł¢Ś¢ŪC.¢Ś¢ÜD.¢Ł¢Ū
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,Rt”÷ABCÖŠ,”ĻACB=90”ć,ŌŚŅŌABµÄÖŠµćOĪŖ×ų±źŌµć,ABĖłŌŚÖ±ĻßĪŖxÖį½ØĮ¢µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠ,½«”÷ABCČʵćBĖ³Ź±ÕėŠż×Ŗ,Ź¹µćAŠż×ŖÖĮyÖįµÄÕż°ėÖįÉĻµÄA“¦,ČōAO=OB=2,ŌņŅõÓ°²æ·ÖĆ껿ĪŖ( )
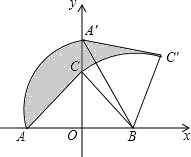
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĆüĢāÕżČ·µÄøöŹżŹĒ
¢ŁČō“śŹżŹ½![]() ÓŠŅāŅ壬ŌņxµÄȔֵ·¶Ī§ĪŖx”Ü1ĒŅx”Ł0£®
ÓŠŅāŅ壬ŌņxµÄȔֵ·¶Ī§ĪŖx”Ü1ĒŅx”Ł0£®
¢ŚĪŅŹŠÉśĢ¬ĀĆÓĪ³õ²½ŠĪ³É¹ęÄ££¬2012ğȫğɜĢ¬ĀĆÓĪŹÕČėĪŖ302 600 000ŌŖ£¬±£ĮōČżøöÓŠŠ§Źż×ÖÓĆæĘѧ¼ĒŹż·Ø±ķŹ¾ĪŖ3.03”Į108ŌŖ£®
¢ŪČō·“±ČĄżŗÆŹż![]() £ØmĪŖ³£Źż£©£¬µ±x£¾0Ź±£¬yĖęxŌö“ó¶ųŌö“ó£¬ŌņŅ»“ĪŗÆŹży=©2x+mµÄĶ¼ĻóŅ»¶Ø²»¾¹żµŚŅ»ĻóĻŽ£®
£ØmĪŖ³£Źż£©£¬µ±x£¾0Ź±£¬yĖęxŌö“ó¶ųŌö“ó£¬ŌņŅ»“ĪŗÆŹży=©2x+mµÄĶ¼ĻóŅ»¶Ø²»¾¹żµŚŅ»ĻóĻŽ£®
¢ÜČōŗÆŹżµÄĶ¼Ļó¹ŲÓŚyÖį¶Ō³Ę£¬ŌņŗÆŹż³ĘĪŖżŗÆŹż£¬ĻĀĮŠČżøöŗÆŹż£ŗy=3£¬y=2x+1£¬y=x2֊żŗÆŹżµÄøöŹżĪŖ2øö£®
A£®1 B£®2 C£®3 D£®4
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com