
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2 , …,Bn , 以线段AnBn为边向左作正方形AnBnCnDn , 如果这组抛物线中的某一条经过点Dn , 求此时满足条件的正方形AnBnCnDn的边长.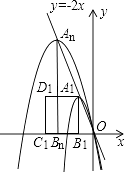
【答案】
(1)解:∵抛物线y=ax2+bx经过点(﹣2,0)和(﹣1,3),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线的表达式为y=﹣3x2﹣6x;
(2)解:∵抛物线y=ax2+bx的顶点坐标是(﹣ ![]() ,﹣
,﹣ ![]() ),且该点在直线y=﹣2x上,
),且该点在直线y=﹣2x上,
∴﹣ ![]() =﹣2×(﹣
=﹣2×(﹣ ![]() ),
),
∵a≠0,∴﹣b2=4b,
解得b1=﹣4,b2=0;
(3)解:这组抛物线的顶点A1、A2、…,An在直线y=﹣2x上,
由(2)可知,b=4或b=0.
①当b=0时,抛物线的顶点在坐标原点,不合题意,舍去;
②当b=﹣4时,抛物线的表达式为y=ax2﹣4x.
由题意可知,第n条抛物线的顶点为An(﹣n,2n),则Dn(﹣3n,2n),
∵以An为顶点的抛物线不可能经过点Dn,设第n+k(k为正整数)条抛物线经过点Dn,此时第n+k条抛物线的顶点坐标是An+k(﹣n﹣k,2n+2k),
∴﹣ ![]() =﹣n﹣k,∴a=
=﹣n﹣k,∴a= ![]() =﹣
=﹣ ![]() ,
,
∴第n+k条抛物线的表达式为y=﹣ ![]() x2﹣4x,
x2﹣4x,
∵Dn(﹣3n,2n)在第n+k条抛物线上,
∴2n=﹣ ![]() ×(﹣3n)2﹣4×(﹣3n),解得k=
×(﹣3n)2﹣4×(﹣3n),解得k= ![]() n,
n,
∵n,k为正整数,且n≤12,
∴n1=5,n2=10.
当n=5时,k=4,n+k=9;
当n=10时,k=8,n+k=18>12(舍去),
∴D5(﹣15,10),
∴正方形的边长是10.
【解析】由已知条件把点(-2,0)和(-1,3)分别代入y=ax2+bx,得到关于a、b的二元一次方程组,解方程组即可得到所求结论;
(2)根据二次函数的性质,得出抛物线y=ax2+bx的顶点坐标是代入,y=-2x,进行计算求值即可;
(3)由于这组抛物线的顶点A1、A2、…,An在直线y=-2x上,根据(2)的结论可知,b=-4或b=0.①当b=0时,不合题意舍去;②当b=-4时,抛物线的表达式为y=ax2-4x.由题意可知,第n条抛物线的顶点为An(-n,2n),则Dn(-3n,2n),因为以An为顶点的抛物线不可能经过点Dn,设第n+k(k为正整数)条抛物线经过点Dn,此时第n+k条抛物线的顶点坐标是An+k(-n-k,2n+2k),通过代入求值即可得到正方形的边长.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE
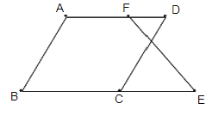
证明:∵∠B+∠BCD=180°(已知)
∴AB∥CD( )
∴∠B=∠DCE( )
又∵∠B=∠D(已知 ),
∴___________ (等量代换)
∴ ∥
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
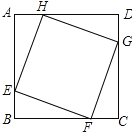
A. 30 B. 34 C. 36 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
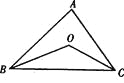
【题目】如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE =12,CE =5,则平行四边形ABCD的周长是______.
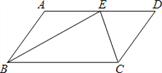
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把三角形ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
(1)画出△A′B′C′;并直接写出点A′、B′、C′的坐标;
(2)若点P(m,n)是△ABC某边上的点,经上述平移后,点P的对应点为P′,写出点P′的坐标(用含m,n的式子表示).
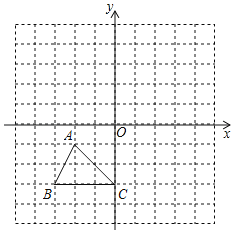
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3)在a的取值范围内,m是最大的整数,n是最小的整数,求(m+n)m-n的值;
(4)在a的取值范围内,当a取何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com