
| A. | 图象过(1,2)点 | B. | 图象在第一、三象限 | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
分析 反比例函数y=$\frac{k}{x}$(k≠0)的图象k>0时位于第一、三象限,在每个象限内,y随x的增大而减小;k<0时位于第二、四象限,在每个象限内,y随x的增大而增大;在不同象限内,y随x的增大而增大,根据这个性质选择则可.
解答 解:∵k=-2<0,所以函数图象位于二四象限,在每一象限内y随x的增大而增大,图象是轴对称图象,故A、B、C错误.
故选D.
点评 本题考查了反比例函数图象的性质:①、当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.②、当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大.注意反比例函数的图象应分在同一象限和不在同一象限两种情况分析.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:填空题
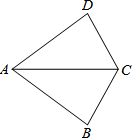 如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是DC=BC或∠DAC=∠BAC.
如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是DC=BC或∠DAC=∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
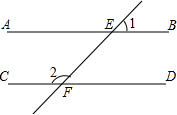 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠2的度数为( )| A. | 43°30′ | B. | 53°30′ | C. | 133°30′ | D. | 153°30′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
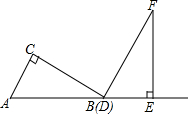 两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com