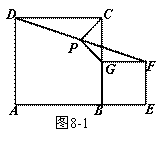
如图8-1，在正方形ABCD和正方形BEFG中，点A，B，E在同一条直线上，连接DF，且P是线段DF的中点，连接PG，PC．
（1）如图8-1中，PG与PC的位置关系是 ，数量关系是 ；（4分）
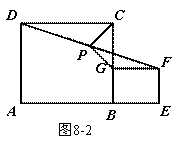
（2） 如图8-2将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变，求证：PG=PC；（4分）
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案科目：初中数学 来源： 题型：
某服装店出售一种羽绒服，每件羽绒服的成本为a元，提价20%后进行出售，则该种羽绒服每件售价为__________________元．（用含a的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
(1)动手操作：
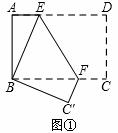
如图①，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点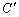
处，折痕为EF，若∠ABE=20°，那么∠
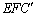的度数为____________．
(2)观察发现：
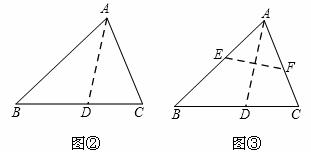
小明将三角形纸片ABC(AB＞AC)沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片(如图②)；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF(如图③)．小明认为△AEF是等腰三角形，你同意吗？请说
明理由．
(3)实践与运用：
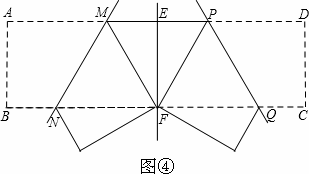
将矩形纸片ABCD 按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP=MN=PQ(如图④)，求∠MNF的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
-
=1
= ． 
若
随
的增大而增大，则
的取值范围是_________________.
