
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

【答案】(1)y=﹣2x+12;y=﹣![]() ;(2)140;(3)x≥10,或﹣4≤x<0;
;(2)140;(3)x≥10,或﹣4≤x<0;
【解析】
(1)根据OA、OB的长写出A、B两点的坐标,再用待定系数法求解一次函数的解析式,然后求得点C的坐标,进而求出反比例函数的解析式.
(2)联立方程组求解出交点坐标即可.
(3)观察函数图象,当函数y=kx+b的图像处于![]() 下方或与其有重合点时,x的取值范围即为
下方或与其有重合点时,x的取值范围即为![]() 的解集.
的解集.
(1)由已知,OA=6,OB=12,OD=4,
∵CD⊥x轴,
∴OB∥CD,
∴△ABO∽△ACD,
∴![]() ,
,
∴![]() ,
,
∴CD=20,
∴点C坐标为(﹣4,20),
∴n=xy=﹣80.
∴反比例函数解析式为:y=﹣![]() ,
,
把点A(6,0),B(0,12)代入y=kx+b得:![]() ,
,
解得:![]() .
.
∴一次函数解析式为:y=﹣2x+12,
(2)当﹣![]() =﹣2x+12时,解得,
=﹣2x+12时,解得,
x1=10,x2=﹣4,
当x=10时,y=﹣8,
∴点E坐标为(10,﹣8),
∴S△CDE=S△CDA+S△EDA=![]() .
.
(3)不等式kx+b≤![]() ,从函数图象上看,表示一次函数图象不低于反比例函数图象,
,从函数图象上看,表示一次函数图象不低于反比例函数图象,
∴由图象得,x≥10,或﹣4≤x<0.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,已知△ABC为等边三角形,动点D在边AC上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连结AP、BD交于Q,两点运动的过程中,AP=BD成立吗?请证明你的结论.
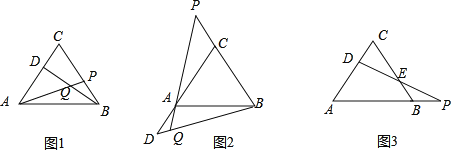
(2)如果把原题中的“动点D在边AC上,动点P在边BC上,”改为:“动点D在射线CA上、动点P在射线BC上运动,”其他条件不变,如图2所示,AP=BD还成立吗?说明理由,并求出∠BQP的大小.
(3)如果把原题中的“动点P在边BC上”,改为“动点P在射线AB上运动”,连结DP交BC于E,其他条件不变,如图3,则动点D、P在运动过程中,请你写出DE与PE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
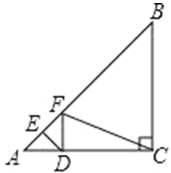
【题目】动手操作:如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=4,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F.当△DFC是直角三角形时,AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填写下表,观察被开方数![]() 的小数点与算术平方根
的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
| 0.0016 | 0.16 | 16 | 1600 |
| 0.04 | 0.4 |
(2)根据你发现的规律填空:
①已知![]() ,则
,则![]() .
.
②已知![]() ,
,![]() ,则
,则![]() 是
是![]() 的 倍.
的 倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)(6x-1)2=25;
(2)x2-2x=2x-1;
(3)x2-![]() x=2;
x=2;
(4)x(x-7)=8(7-x).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论①△AEF≌△AED;②∠AED=45°;③BE+DC=DE; ④BE![]() +DC
+DC![]() =DE
=DE![]() ,其中正确的是( )
,其中正确的是( )

A. ②④ B. ①④ C. ②③ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com