
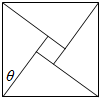
 (2012•岱岳区二模)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么cosθ的值是
(2012•岱岳区二模)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么cosθ的值是7
| ||
| 74 |
7
| ||
| 74 |
| 74 |
| 2 |
| 74 |
| 4 |
| 35 |
| 2 |
| 1 |
| 2 |
| 35 |
| 2 |
|
| 7 | ||
|
7
| ||
| 74 |
7
| ||
| 74 |


科目:初中数学 来源: 题型:
 (2012•岱岳区二模)半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2
(2012•岱岳区二模)半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
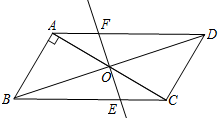 (2012•岱岳区二模)已知,如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=
(2012•岱岳区二模)已知,如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
(2012•岱岳区二模)2011年11月份,鹿城区环境检测中心的关于“水心菜篮子”某一周空气质量报告中某项污染指数的数据如表所示,这组数据的众数是( )
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com