
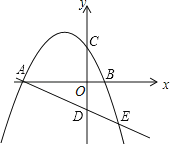
【题目】如图,已知二次函数y=ax2+4ax+c(a≠0)的图象交x轴于A、B两点(A在B的左侧),交y轴于点C.一次函数y=﹣![]() x+b的图象经过点A,与y轴交于点D(0,﹣3),与这个二次函数的图象的另一个交点为E,且AD:DE=3:2.
x+b的图象经过点A,与y轴交于点D(0,﹣3),与这个二次函数的图象的另一个交点为E,且AD:DE=3:2.
(1)求这个二次函数的表达式;
(2)若点M为x轴上一点,求MD+![]() MA的最小值.
MA的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先把D点坐标代入y=﹣![]() x+b中求得b,则一次函数解析式为y=﹣
x+b中求得b,则一次函数解析式为y=﹣![]() x﹣3,于是可确定A(﹣6,0),作EF⊥x轴于F,如图,利用平行线分线段成比例求出OF=4,接着利用一次函数解析式确定E点坐标为(4,﹣5),然后利用待定系数法求抛物线解析式;
x﹣3,于是可确定A(﹣6,0),作EF⊥x轴于F,如图,利用平行线分线段成比例求出OF=4,接着利用一次函数解析式确定E点坐标为(4,﹣5),然后利用待定系数法求抛物线解析式;
(2)作MH⊥AD于H,作D点关于x轴的对称点D′,如图,则D′(0,3),利用勾股定理得到AD=3![]() ,再证明Rt△AMH∽Rt△ADO,利用相似比得到MH=
,再证明Rt△AMH∽Rt△ADO,利用相似比得到MH=![]() AM,加上MD=MD′,MD+
AM,加上MD=MD′,MD+![]() MA=MD′+MH,利用两点之间线段最短得到当点M、H、D′共线时,MD+
MA=MD′+MH,利用两点之间线段最短得到当点M、H、D′共线时,MD+![]() MA的值最小,然后证明Rt△DHD′∽Rt△DOA,利用相似比求出D′H即可.
MA的值最小,然后证明Rt△DHD′∽Rt△DOA,利用相似比求出D′H即可.
解:(1)把D(0,﹣3)代入y=﹣![]() x+b得b=﹣3,
x+b得b=﹣3,
∴一次函数解析式为y=﹣![]() x﹣3,
x﹣3,
当y=0时,﹣![]() x﹣3=0,解得x=﹣6,则A(﹣6,0),
x﹣3=0,解得x=﹣6,则A(﹣6,0),
作EF⊥x轴于F,如图,
∵OD∥EF,
∴![]() =
=![]() =
=![]() ,
,
∴OF=![]() OA=4,
OA=4,
∴E点的横坐标为4,
当x=4时,y=﹣![]() x﹣3=﹣5,
x﹣3=﹣5,
∴E点坐标为(4,﹣5),
把A(﹣6,0),E(4,﹣5)代入y=ax2+4ax+c得![]() ,解得
,解得 ,
,
∴抛物线解析式为![]() ;
;
(2)作MH⊥AD于H,作D点关于x轴的对称点D′,如图,则D′(0,3),
在Rt△OAD中,AD=![]() =3
=3![]() ,
,
∵∠MAH=∠DAO,
∴Rt△AMH∽Rt△ADO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴MH=![]() AM,
AM,
∵MD=MD′,
∴MD+![]() MA=MD′+MH,
MA=MD′+MH,
当点M、H、D′共线时,MD+![]() MA=MD′+MH=D′H,此时MD+
MA=MD′+MH=D′H,此时MD+![]() MA的值最小,
MA的值最小,
∵∠D′DH=∠ADO,
∴Rt△DHD′∽Rt△DOA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得D′H=
,解得D′H=![]() ,
,
∴MD+![]() MA的最小值为
MA的最小值为![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
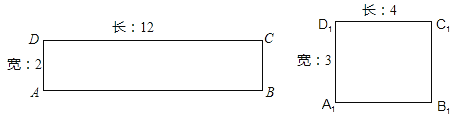
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图矩形![]() 是矩形ABCD的“减半”矩形.
是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式是y=x2﹣(k+2)x+2k﹣2.
(1)求证:此抛物线与x轴必有两个不同的交点;
(2)若抛物线与直线y=x+k2﹣1的一个交点在y轴上,求该二次函数的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)根据上述信息可知:甲命中环数的中位数是_____环,乙命中环数的众数是______环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会变小.(填“变大”、“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
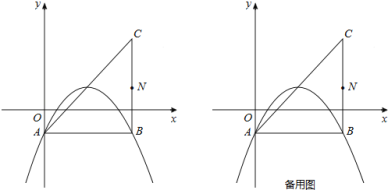
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末![]() 位能被
位能被![]() 整除的数,本身必能被
整除的数,本身必能被![]() 整除,反过来,末
整除,反过来,末![]() 位不能被
位不能被![]() 整除的数,本身也不可能被
整除的数,本身也不可能被![]() 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
![]() ,
,![]() 为整数,
为整数,![]() 能被25整除
能被25整除
![]() ,
,![]() 不为整数,
不为整数,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若![]() 这个三位数能被11整除,则
这个三位数能被11整除,则![]() ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
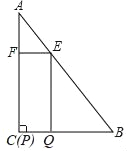
【题目】如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).
(1)当AE=8时,求EF的长;
(2)设AE=x,矩形EFPQ的面积为y.
①求y与x的函数关系式;
②当x为何值时,y有最大值,最大值是多少?
(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com