【题目】计算：
（1）（
x2y-2xy+y2）（-4xy）；
（2）6mn2(2－
mn4)＋(－mn3)2；
（3）-4x2·（xy-y2）-3x·（xy2-2x2y）；
（4）
．
【答案】（1）-2x3y2+8x2y2-4xy3；（2）12mn2－
m2n6（3）4x3y+x2y2（4）2x2
【解析】
利用单项式乘多项式法则计算得出．
（1）（
x2y-2xy+y2）·（-4xy）
=x2y·（-4xy）+(-2xy)·（-4xy）+ y2·（-4xy）
=-2x3y2+8x2y2-4xy3
（2）6mn2(2－
mn4)＋(－mn3)2
=6mn2×2+6mn2×(－mn4)＋
m2n6
=12mn2－m2n6
（3）-4x2·（xy-y2）-3x·（xy2-2x2y）
=-4x2·xy+(-4x2)·（-y2）-3x·xy2-3x·（-2x2y）
=-2x3y+4x2y2-3x2y2+6x3y
=4x3y+x2y2
（4）
=x+x2-x-x2
=2x2
一诺书业暑假作业快乐假期云南美术出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，折线ABC是在某市乘出租车所付车费y（元）与行车里程x（km）之间的函数关系图象．
（1）根据图象，求当x≥3时的函数关系式；
（2）某人乘坐2.5km，应付多少钱？
（3）某人乘坐13km，应付多少钱？
（4）若某人付车费30.8元，出租车行驶了多少路程？
查看答案和解析>>
科目：初中数学 来源： 题型：
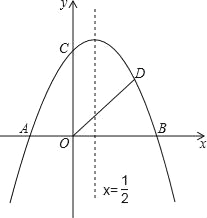
【题目】如图，抛物线y=﹣
x2+bx+c与x轴交于A、B两点（A在B点左侧），与y轴交于点C，对称轴为直线x=
，OA=2，OD平分∠BOC交抛物线于点D（点D在第一象限）；
（1）求抛物线的解析式和点D的坐标；
（2）点M是抛物线上的动点，在x轴上存在一点N，使得A、D、M、N四个点为顶点的四边形是平行四边形，求出点M的坐标；
（3）在抛物线的对称轴上，是否存在一点P，使得△BPD的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
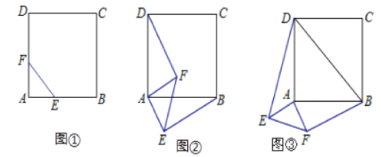
【题目】（1）如图①，正方形ABCD，点E、点F分别在AB和AD上，且AE=AF．此时，线段BE、DF的数量关系是 ，位置关系是 ．请直接写出结论．
(2)如图②,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立，如果成立，请证明；如果不成立，请说明理由。
(3)如图③,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时，连接BD、DE、EF、FB，得到四边形BDEF，则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
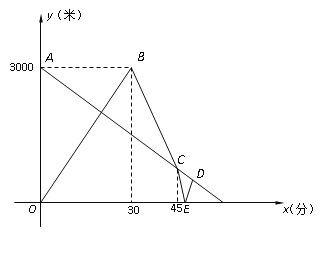
【题目】小明从家去体育场锻炼，同时，妈妈从体育场以50米/分的速度回家，小明到体育场后发现要下雨，立即返回，追上妈妈后，小明以250米/分的速度回家取伞，立即又以250米/分的速度折回接妈妈，并一同回家．如图是两人离家的距离y（米）与小明出发的时间x（分）之间的函数图像．
（注：小明和妈妈始终在同一条笔直的公路上行走，图像上A、C、D三点在一条直线上）
（1）求线段BC的函数表达式；
（2）求点D坐标；
（3）当 x的值为 时，小明与妈妈相距1 500米．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形纸片ABCD中，AB＝4，BC＝8，将纸片沿EF折叠，使点C与点A重合，则下列结论错误的是（ ）
A. AF＝AE B. △ABE≌△AGF C. EF＝
D. AF＝EF
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于一个大于1的正整数n进行如下操作：
① 将n拆分为两个正整数a、b的和，并计算乘积a×b
② 对于正整数a、b分别重复此操作，得到另外两个乘积
③ 重复上述过程，直至不能再拆分为止（即拆分到正整数1）
当n＝6时，所有的乘积的和为_________，当n＝100时，所有的乘积的和为_________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数的图象经过点A(2,0),B(0,4).
（1）求此函数的解析式；
（2）若点P为此一次函数图象上一动点，且△POA的面积为2，求点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场同时购进甲、乙两种商品共200件，其进价和售价如表，
商品名称 | 甲 | 乙 |
进价（元/件） | 80 | 100 |
售价（元/件） | 160 | 240 |
设其中甲种商品购进x件，该商场售完这200件商品的总利润为y元．
（1）求y与x的函数关系式；
（2）该商品计划最多投入18000元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com