【小题1】背景 ：在图1中，已知线段AB，CD。其中点分别是E，F。
①若A（-1,0），B（3,0），则E点的坐标为________;
②若C（-2,2），D（-2,-1），则F点的坐标为_________;
【小题2】探究： 在图2中，已知线段AB的端点坐标A（a,b）,B(c,d),求出图中AB中点D的坐标（用含a,b,c,d的代数式表示），并给出求解过程；
归纳： 无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（a,b）,B(c,d),AB中点为D（x,y）时，x=______,y=_________(不必证明)。
运用： 在图3中，一次函数y=x-2与反比例函数
的图像交点为A，B。
①求出交点A,B的坐标；
②若以A、O、B、P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标。
科目：初中数学 来源： 题型：
的图像交点为A，B。
查看答案和解析>>
科目：初中数学 来源： 题型：
中，
、
、
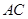三边的长分别为
、
、
，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图①所示．这样不需求的高，而借用网格就能计算出它的面积．的面积直接填写在横线上．_________________________思维拓展：面积的方法叫做构图法．若 三边的长分别为
、
、
（
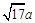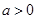），请利用图②的正方形网格（每个小正方形的边长为
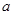）画出相应的，并求出它的面积．探索创新：三边的长分别为
、
、
（
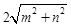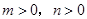，且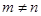
），试运用构图法求出这三角形的面积．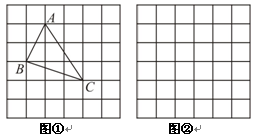
查看答案和解析>>
科目：初中数学 来源：2011-2012学年浙江省杭州市萧山瓜沥片八年级12月月考数学卷 题型：解答题
问题背景：在△ABC中，AB、BC、AC三边的长分别为、、，
求这个三角形的面积．
小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处)，如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面
积．
【小题1】(1)请你将△ABC的面积直接填写在横线上．____ ▲__
_____
【小题2】(2)我们把上述求△ABC面积的方法叫做构图法．若△ABC三边的长分别为a、2a、a(a＞0)，请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC，并求出它的面积．
【小题3】(3)若△ABC三边的长分别为、、2(m＞0，n＞0，且m≠n)，试运用构图法求出这三角形的面积．
查看答案和解析>>
科目：初中数学 来源：2012届浙江省金华市浦江五中九年级下学期月考数学卷 题型：解答题
题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．
问题探究：
【小题1】（1）①如图1所示，当G在CD边上时，猜想线段BG、DE的数量关系及所在直线的位置关系．（不要求证明）
②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，请选择图2或图3证明你的判断．
类比研究：
【小题2】（2）若将原题中的“正方形”改为“矩形”（如图所示），且
=k（其中k＞0），请写出 线段BG、DE的数量关系及位置关系．请选择图5或图6证明你的判断（仅证数量关系）．
拓展应用：
【小题3】（3）在（1）中图2中，连接DG、BE，若AB=3，EF=2，求BE2+DG2的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
………………………………………………………………………….6分
解得：
。由题意得A（-1，-3），B（3,1）。② AB为对角线时P(2，-2); AO为对角线时P(-4，-4); BO为对角线时P(4，-4);…………….10分
