
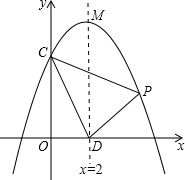
 如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,
如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,分析 (1)由OC与OD的长,求出MD的长,确定出M坐标,设y=a(x-2)2+6,把C坐标代入求出a的值,即可确定出抛物线解析式;
(2)由抛物线解析式设出P坐标,过点P做x轴的垂线,交x轴于点E,利用表示出的点P的坐标确定出线段PE、DE的长,用梯形OCPE的面积减去直角三角形OCD的面积和直角三角形PDE的面积,进而得出S与x的函数解析式,利用二次函数性质求出S最大值时x的值即可.
解答 解:(1)∵OC=4,OD=2,
∴DM=6,
∴点M(2,6),
设y=a(x-2)2+6,代入(0,4)得:a=-$\frac{1}{2}$,
∴该抛物线解析式为y=-$\frac{1}{2}$(x-2)2+6;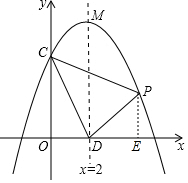
(2)设点P(x,-$\frac{1}{2}$ (x-2)2+6),即(x,-$\frac{1}{2}$x2+2x+4),x>0,
过点P作x轴的垂线,交x轴于点E,
则PE=-$\frac{1}{2}$x2+2x+4,DE=x-2,
S=$\frac{1}{2}$x(-$\frac{1}{2}$x2+2x+4+4)-$\frac{1}{2}$×2×4-$\frac{1}{2}$(x-2)(-$\frac{1}{2}$x2+2x+4),
即S=-$\frac{1}{2}$x2+4x=-$\frac{1}{2}$(x-4)2+8,
∴当x=4时,S有最大值为8.
点评 此题考查了待定系数法求二次函数解析式,以及二次函数的最值,熟练掌握待定系数法是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 决赛成绩(单位:分) | |
| 七年级 | 82 86 88 81 88 97 80 74 90 89 |
| 八年级 | 85 88 87 97 85 76 88 80 86 88 |
| 九年级 | 81 83 79 79 79 92 99 88 89 86 |
| 年纪 | 平均数 | 众数 | 中位数 |
| 七年级 | 85.5 | 88 | 87 |
| 八年级 | 86 | 88 | 86.5 |
| 九年级 | 85.5 | 79 | 84.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
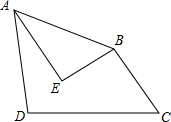 如图,在四边形ABCD中,AB=AD,∠BAD=∠C=60°,点E为四边形ABCD内部一点,连接AE、BE,∠AEB=∠CBE=90°,BC=3,则线段BE的长为$\frac{3\sqrt{3}}{2}$.
如图,在四边形ABCD中,AB=AD,∠BAD=∠C=60°,点E为四边形ABCD内部一点,连接AE、BE,∠AEB=∠CBE=90°,BC=3,则线段BE的长为$\frac{3\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com