
【题目】如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为_______.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】开学初,小聪去某文具商店购买学习用品的数据如下表(因污损导致部分数据无法识别):
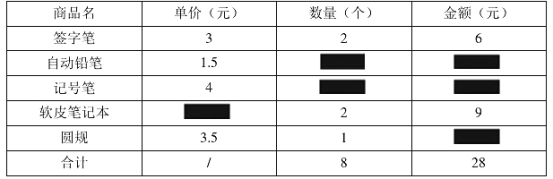
仔细观察表格中数据之间的关系,解决下列问题:
(1)这家文具商店软面笔记本的单价是________元/本,小聪购买圆规共花费______元;
(2)小聪购买了自动铅笔、记号笔各几支?
(3)若小明也在同一家文具店购买了软面笔记本和自动铅笔两种文具,已知他恰好花费12元,请你对小明购买的软面笔记本和自动铅笔数量的可能性进行分析。
查看答案和解析>>
科目:初中数学 来源: 题型:
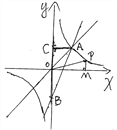
【题目】如图,P是反比例函数y= ![]() (k>0)的图像在第一象限上的一个动点,过P作z轴的垂线,垂足为M,已知△POM的面积为2.
(k>0)的图像在第一象限上的一个动点,过P作z轴的垂线,垂足为M,已知△POM的面积为2.
(l)求k的值;
(2)若直线y=x与反比例函数y=![]() 的图像在第一象限内交于点A,求过点A和点B(0,-2)的直线表达式;
的图像在第一象限内交于点A,求过点A和点B(0,-2)的直线表达式;
(3)过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解满足x为非正数,y为负数.
的解满足x为非正数,y为负数.
(1)求m的取值范围;
(2)化简:|m﹣3|﹣|m+2|;
(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
(1)当t=1时,KE=_____,EN=_____;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
(4)当t为何值时,△PKB是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
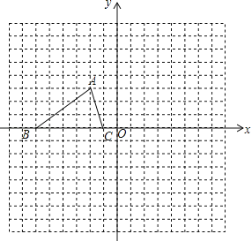
【题目】如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′的坐标_____;
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点A″的坐标_____;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从![]() ,
,![]() 两地相向而行,他们距
两地相向而行,他们距![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系如图所示,下列说法错误的是( )
的关系如图所示,下列说法错误的是( )

A.甲的速度是![]() B.甲出发4.5小时后与乙相遇
B.甲出发4.5小时后与乙相遇
C.乙比甲晚出发2小时D.乙的速度是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠ADC= 度;
(2)当∠C=20°时,判断DE与AC的位置关系,并说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com