
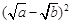 ≥0, ∴
≥0, ∴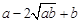 ≥0,
≥0,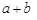 ≥
≥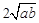 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.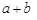 ≥
≥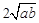 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥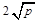 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值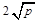 .
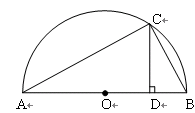
.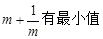 .
.
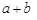 ≥
≥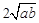 ,并指出等号成立时的条件.
,并指出等号成立时的条件. 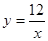 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.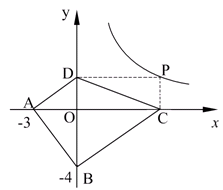
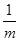 不扣分),最小值为 2 ;
不扣分),最小值为 2 ; 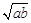
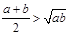 ,
, 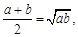
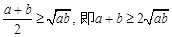 ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.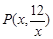 , 则
, 则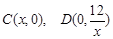 ,
,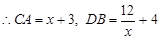 ,
,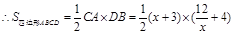 ,化简得:
,化简得: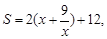
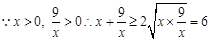 ,只有当
,只有当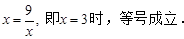
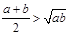 ;若点D与O重合,
;若点D与O重合,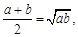
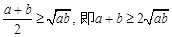 ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
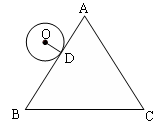
| A.2周 | B.3周 | C.4周 | D.5周 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
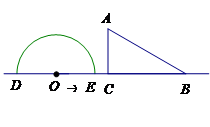
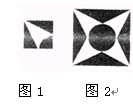
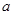 ,圆心在原点的圆(如图1),如果固定直径
,圆心在原点的圆(如图1),如果固定直径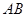 ,把圆内的所有与
,把圆内的所有与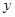 轴平行的弦都压缩到原来的
轴平行的弦都压缩到原来的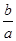 倍,就得到一种新的图形
倍,就得到一种新的图形 椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .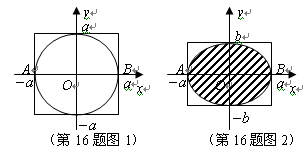
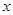 轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为
轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为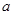 的球的体积为
的球的体积为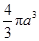 ,则此椭球的体积为 .
,则此椭球的体积为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com