
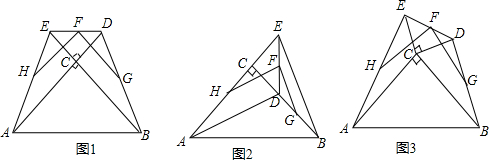
分析 (1)证AD=BE,根据三角形的中位线推出FH=$\frac{1}{2}$AD,FH∥AD,FG=$\frac{1}{2}$BE,FG∥BE,即可推出答案;
(2)①证△ACD≌△BCE,推出AD=BE,根据三角形的中位线定理即可推出答案;
②连接BE、AD,根据全等推出AD=BE,根据三角形的中位线定理即可推出答案;
(3)如图4中,由题意,易知CF⊥DE,△CFD,△CFE都是等腰直角三角形,由CD=$\sqrt{2}$,推出CF=DF=1,∵BC=AC=2,推出BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=$\sqrt{3}$,推出BD=BF-DF=$\sqrt{3}$-1,由DG=GB,推出DG=$\frac{1}{2}$($\sqrt{3}$-1),根据FG=DF+DG计算即可解决问题;
解答 (1)解:如图1中,
∵CE=CD,AC=BC,∠ECA=∠DCB=90°,
∴BE=AD,
∵F是DE的中点,H是AE的中点,G是BD的中点,
∴FH=$\frac{1}{2}$AD,FH∥AD,FG=$\frac{1}{2}$BE,FG∥BE,
∴FH=FG,
∵AD⊥BE,
∴FH⊥FG,
故答案为:FG=FH,FG⊥FH.
(2)①答:成立,
证明:如图2中,
∵CE=CD,∠ECD=∠ACD=90°,AC=BC,
∴△ACD≌△BCE
∴AD=BE,
由(1)知:FH=$\frac{1}{2}$AD,FH∥AD,FG=$\frac{1}{2}$BE,FG∥BE,
∴FH=FG,FH⊥FG,
∴(1)中的猜想还成立.
②答:成立,结论是FH=FG,FH⊥FG.
如图3中,连接AD,BE,两线交于Z,AD交BC于X,
同(1)可证
∴FH=$\frac{1}{2}$AD,FH∥AD,FG=$\frac{1}{2}$BE,FG∥BE,
∵三角形ECD、ACB是等腰直角三角形,
∴CE=CD,AC=BC,∠ECD=∠ACB=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CE=CD}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE,∠EBC=∠DAC,
∵∠DAC+∠CXA=90°,∠CXA=∠DXB,
∴∠DXB+∠EBC=90°,
∴∠EZA=180°-90°=90°,
即AD⊥BE,
∵FH∥AD,FG∥BE,
∴FH⊥FG,
即FH=FG,FH⊥FG,
结论是FH=FG,FH⊥FG.
(3)如图4中,
由题意,易知CF⊥DE,△CFD,△CFE都是等腰直角三角形,
∵CD=$\sqrt{2}$,
∴CF=DF=1,∵BC=AC=2,
∴BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=$\sqrt{3}$,
∴BD=BF-DF=$\sqrt{3}$-1,
∵DG=GB,
∴DG=$\frac{1}{2}$($\sqrt{3}$-1),
∴FG=DF+DG=$\frac{\sqrt{3}+1}{2}$.
点评 本题主要考查对等腰直角三角形的性质,全等三角形的性质和判定,三角形的中位线定理,旋转的性质等知识点的理解和掌握,能熟练地运用这些性质进行推理是解此题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
| 射击总次数n | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| 击中靶心次数m | 9 | 16 | 41 | 88 | 168 | 429 | 861 |
| 击中靶心频率 $\frac{m}{n}$ | 0.9 | 0.8 | 0.82 | 0.88 | 0.84 | 0.858 | 0.861 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价x元/公斤 | … | 30 | 35 | 40 | 45 | … |
| 销售量y公斤 | … | 500 | 450 | 400 | 350 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
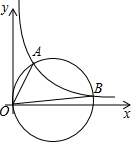 如图,点A(1,2)在反比例函数y=$\frac{k}{x}$(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
如图,点A(1,2)在反比例函数y=$\frac{k}{x}$(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )| A. | (2,1) | B. | (3,$\frac{2}{3}$) | C. | (4,0.5) | D. | (5,0.4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 190×lO8 | B. | 1.9×1010 | C. | 0.19×1011 | D. | 19×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{12}$ | C. | $\sqrt{7}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com