
 如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上.
如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上. 分析 连接DA、DB,根据线段垂直平分线的性质得到DA=DB,证明Rt△DAN≌Rt△BDM,得到DN=DM,证明Rt△NDC≌Rt△MDC,得到答案.
解答 证明:连接DA、DB,
∵DE⊥AB,E为△ABC中AB边的中点,
∴DA=DB,
在Rt△DAN和Rt△BDM中,
$\left\{\begin{array}{l}{DA=DB}\\{AN=BM}\end{array}\right.$,
∴Rt△DAN≌Rt△BDM,
∴DN=DM,
在Rt△NDC和Rt△MDC中,
$\left\{\begin{array}{l}{DN=DM}\\{DC=DC}\end{array}\right.$,
∴Rt△NDC≌Rt△MDC,
∴∠NDC=∠MDC,
∴点D在△ABC的外角平分线上.
点评 本题考查的是线段垂直平分线的性质、全等三角形的判定和性质,掌握线段垂直平分线上的点与线段两个端点的距离相等是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
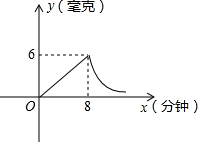 为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题:
为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面积为2000平方米的长方形临时仓库,并在其中一边上留宽为3米的大门,求无门的那边长.
如图,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面积为2000平方米的长方形临时仓库,并在其中一边上留宽为3米的大门,求无门的那边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知有理数a,b,c在数轴上的位置如图所示,请化简:
已知有理数a,b,c在数轴上的位置如图所示,请化简:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com