
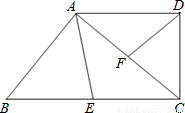
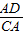 =
=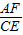 ;
; =10;
=10; AC=5;
AC=5; =
=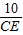 ,解得CE=
,解得CE=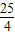 ;
;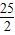 ;
; ×(
×(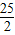 +8)×6=
+8)×6=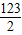 .
.

科目:初中数学 来源:2010年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
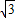 ,1)、C(-3
,1)、C(-3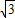 ,0)、O(0,0).将此矩形沿着过E(-
,0)、O(0,0).将此矩形沿着过E(-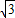 ,1)、F(-
,1)、F(-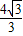 ,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.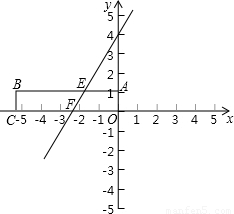
查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市中考数学试卷(解析版) 题型:解答题
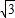 ,1)、C(-3
,1)、C(-3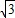 ,0)、O(0,0).将此矩形沿着过E(-
,0)、O(0,0).将此矩形沿着过E(-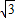 ,1)、F(-
,1)、F(-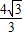 ,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.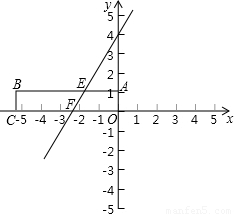
查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市义桥实验学校中考数学模拟试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2011年湖北省武汉六中中考数学模拟试卷(3月份)(解析版) 题型:选择题
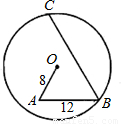
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com