
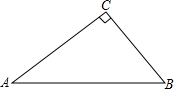
 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.若P、Q分别是AB和AC上的动点,则PC+PQ的最小值是$\frac{192}{25}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.若P、Q分别是AB和AC上的动点,则PC+PQ的最小值是$\frac{192}{25}$. 分析 作点C关于AB的对称点D,过D作DQ⊥AC于Q,则DQ的长度即为PC+PQ的最小值,由勾股定理得到AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,根据三角形的面积求得CD=2×$\frac{AC•BC}{AB}$=$\frac{48}{5}$,通过△DQC∽△ABC,得到$\frac{CD}{AB}=\frac{DQ}{AC}$,代入数据即可得到结论.
解答 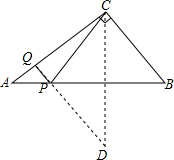 解:作点C关于AB的对称点D,过D作DQ⊥AC于Q,则DQ的长度即为PC+PQ的最小值,
解:作点C关于AB的对称点D,过D作DQ⊥AC于Q,则DQ的长度即为PC+PQ的最小值,
∵∠ACB=90°,AB=10,BC=6,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
∴CD=2×$\frac{AC•BC}{AB}$=$\frac{48}{5}$,
∵∠D+∠DCQ=90°,∠A+∠ACD=90°,
∴∠A=∠D,
∵∠DQC=∠ACB=90°,
∴△DQC∽△ABC,
∴$\frac{CD}{AB}=\frac{DQ}{AC}$,
即$\frac{\frac{48}{5}}{10}=\frac{DQ}{8}$,
∴DQ=$\frac{192}{25}$.
∴PC+PQ的最小值是$\frac{192}{25}$.
故答案为:$\frac{192}{25}$.
点评 此题主要考查轴对称--最短路线问题,相似三角形的判定和性质,三角形的面积,正确的作出图形是解题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
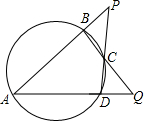 如图,点A、B、C,D在同一圆上,AD,BC延长线相交于点Q,AB,DC的延长线相交于点P.若∠A=50°,∠P=35°,则∠Q=45°.
如图,点A、B、C,D在同一圆上,AD,BC延长线相交于点Q,AB,DC的延长线相交于点P.若∠A=50°,∠P=35°,则∠Q=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
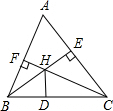 如图,在△ABC中,∠ABC=60°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHD的度数.
如图,在△ABC中,∠ABC=60°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
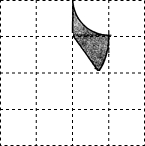 如图,已知网格中每个小正方形的边长都是1,图中的图案由两段以格点为圆心,分别以1和2为半径的圆弧和网格的边围成.
如图,已知网格中每个小正方形的边长都是1,图中的图案由两段以格点为圆心,分别以1和2为半径的圆弧和网格的边围成.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/个) | 10 | 11 | 12 | 13 | … |
| 每周销量(个) | 20 | 18 | 16 | 14 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com