

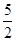 -
- .
.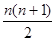 个,即第i行的最后一个数是
个,即第i行的最后一个数是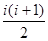 .
.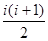 ≥2008的最小正整数解.
≥2008的最小正整数解. =1953,而
=1953,而 =2016,所以,i=63.于是,第63行的第一个数是
=2016,所以,i=63.于是,第63行的第一个数是 +1=1954.故j=(2008—1954)+1=55.
+1=1954.故j=(2008—1954)+1=55.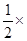
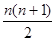 =
=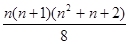
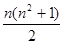 ,∴当n≥2时,
,∴当n≥2时,
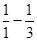 )+(
)+(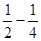 )+(
)+(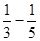 )+…+(
)+…+( )
)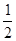 -
- =
=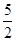 -
- .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com