
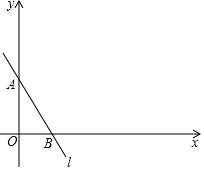
 如图,已知一次函数y=-$\frac{4}{3}$x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.
如图,已知一次函数y=-$\frac{4}{3}$x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.分析 (1)由一次函数解析式容易求得A、B的坐标,利用勾股定理可求得AB的长度;
(2)①根据同角的三角函数得:tan∠OAB=$\frac{OB}{OA}=\frac{EM}{AE}$=$\frac{3}{4}$,设EM=3x,AE=4x,则AM=5x,得M(3x,-4x+4),证明△AHN≌△MEA,则AH=EM=3x,根据NG=OH,列式可得x的值,计算M的坐标即可;
②如图2,先计算E与G重合,易得∠QAP=∠OAB=∠DCE,所以△APQ与△CDE相似时,顶点C必与顶点A对应,可分两种情况进行讨论:
i)当△DCE∽△QAP时,证明△ACO∽△NCE,列比例式可得CO=$\frac{16}{3}$,根据三角函数得:tan∠QNA=tan∠DNF=$\frac{DF}{NF}=\frac{AQ}{AN}$,AQ=20,则tan∠QAH=tan∠OAB=$\frac{3}{4}$=$\frac{QH}{AH}$,设QH=3x,AH=4x,则AQ=5x,
求出x的值,得P(0,14);
ii)当△DCE∽△PAQ时,如图3,先证明B与Q重合,由AN=AP可得P(0,-6).
解答 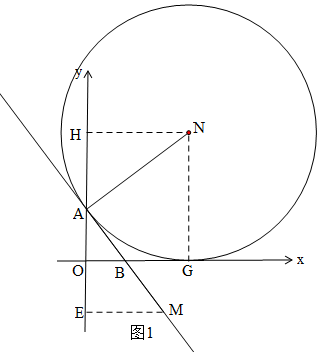 解:(1)当x=0时,y=4,
解:(1)当x=0时,y=4,
∴A(0,4),
∴OA=4,
当y=0时,-$\frac{4}{3}$x+4=0,
x=3,
∴B(3,0),
∴OB=3,
由勾股定理得:AB=5;
(2)①如图1,过N作NH⊥y轴于H,过M作ME⊥y轴于E,
tan∠OAB=$\frac{OB}{OA}=\frac{EM}{AE}$=$\frac{3}{4}$,
∴设EM=3x,AE=4x,则AM=5x,
∴M(3x,-4x+4),
由旋转得:AM=AN,∠MAN=90°,
∴∠EAM+∠HAN=90°,
∵∠EAM+∠AME=90°,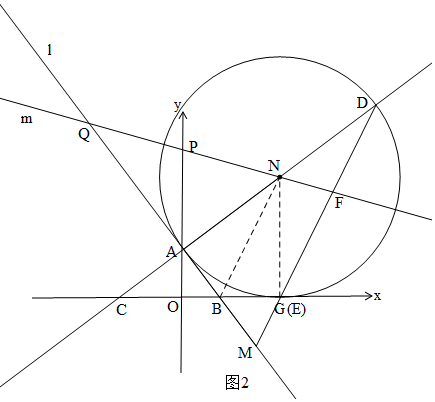
∴∠HAN=∠AME,
∵∠AHN=∠AEM=90°,
∴△AHN≌△MEA,
∴AH=EM=3x,
∵⊙N与x轴相切,设切点为G,连接NG,则NG⊥x轴,
∴NG=OH,
则5x=3x+4,
2x=4,
x=2,
∴M(6,-4);
②如图2,由①知N(8,10),
∵AN=DN,A(0,4),
∴D(16,16),
设直线DM:y=kx+b,
把D(16,16)和M(6,-4)代入得:$\left\{\begin{array}{l}{16k+b=16}\\{6k+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-16}\end{array}\right.$,
∴直线DM的解析式为:y=2x-16,
∵直线DM交x轴于E,
∴当y=0时,2x-16=0,
x=8,
∴E(8,0),
由①知:⊙N与x轴相切,切点为G,且G(8,0),
∴E与切点G重合,
∵∠QAP=∠OAB=∠DCE,
∴△APQ与△CDE相似时,顶点C必与顶点A对应,
分两种情况:
i)当△DCE∽△QAP时,如图2,∠AQP=∠NDE,
∵∠QNA=∠DNF,
∴∠NFD=∠QAN=90°,
∵AO∥NE,
∴△ACO∽△NCE,
∴$\frac{AO}{NE}=\frac{CO}{CE}$,
∴$\frac{4}{10}=\frac{CO}{CO+8}$,
∴CO=$\frac{16}{3}$,
连接BN,
∴AB=BE=5,
∵∠BAN=∠BEN=90°,
∴∠ANB=∠ENB,
∵EN=ND,
∴∠NDE=∠NED,
∵∠CNE=∠NDE+∠NED,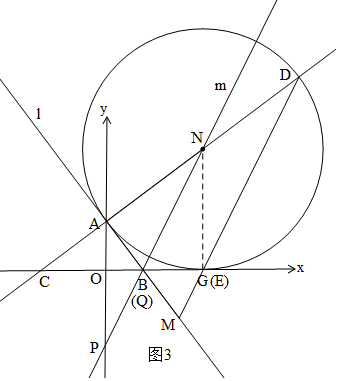
∴∠ANB=∠NDE,
∴BN∥DE,
Rt△ABN中,BN=$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$,
sin∠ANB=∠NDE=$\frac{AB}{BN}=\frac{NF}{DN}$,
∴$\frac{5}{5\sqrt{5}}=\frac{NF}{10}$,
∴NF=2$\sqrt{5}$,
∴DF=4$\sqrt{5}$,
∵∠QNA=∠DNF,
∴tan∠QNA=tan∠DNF=$\frac{DF}{NF}=\frac{AQ}{AN}$,
∴$\frac{4\sqrt{5}}{2\sqrt{5}}=\frac{AQ}{10}$,
∴AQ=20,
∵tan∠QAH=tan∠OAB=$\frac{3}{4}$=$\frac{QH}{AH}$,
设QH=3x,AH=4x,则AQ=5x,
∴5x=20,
x=4,
∴QH=3x=12,AH=16,
∴Q(-12,20),
同理易得:直线NQ的解析式:y=-$\frac{1}{2}$x+14,
∴P(0,14);
ii)当△DCE∽△PAQ时,如图3,
∴∠APN=∠CDE,
∵∠ANB=∠CDE,
∵AP∥NG,
∴∠APN=∠PNE,
∴∠APN=∠PNE=∠ANB,
∴B与Q重合,
∴AN=AP=10,
∴OP=AP-OA=10-4=6,
∴P(0,-6);
综上所述,△APQ与△CDE相似时,点P的坐标的坐标(0,14)或(0,-6).
点评 本题是一次函数的综合题,考查了利用待定系数法求一次函数的解析式、三角形全等和相似的性质和判定、三角函数、直线与坐标轴的交点,并采用了分类讨论的思想解决问题,第(2)问中的2小问有难度,正确画出图形是关键,并确定其相似的对应关系.


科目:初中数学 来源: 题型:选择题
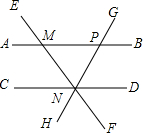 如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )| A. | ∠DNG=∠AME | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠EMB=∠END |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
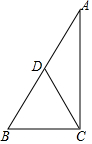 如图Rt△ABC中,∠ACB=90°,D为AB的中点,E在边AB上,AB=12,BC=6,当ED=$\frac{1}{2}$CD,则CE=3$\sqrt{7}$或3$\sqrt{3}$.
如图Rt△ABC中,∠ACB=90°,D为AB的中点,E在边AB上,AB=12,BC=6,当ED=$\frac{1}{2}$CD,则CE=3$\sqrt{7}$或3$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com