
【题目】我们知道,解一元二次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想我们还可以解一些新的方程例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,通过解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”的思想求方程![]() =x的解.
=x的解.
(3)试直接写出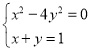 的解 .
的解 .
【答案】(1)1,2;(2)3;(3)![]() ,
,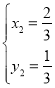 .
.
【解析】
(1)根据题意对方程![]() 进行因式分解即可求出
进行因式分解即可求出![]() 的值.
的值.
(2)先把等号左右两边同时平方,去掉根号,然后进行因式分解即可.
(3)将![]() 用平方差公式拆成
用平方差公式拆成![]() 与
与![]() 组成两个二元一次方程组,解方程组即可.
组成两个二元一次方程组,解方程组即可.
解:(1)∵x3+x2﹣2x=0
∴x(x2+x﹣2)=0,
∴x(x﹣1)(x+2)=0
则x=0或x﹣1=0或x+2=0
解得x1=0,x2=1,x3=﹣2,
故答案为1,2;
(2)∵![]() =x,
=x,
∴2x+3=x2(x≥0),即x2﹣2x﹣3=0,
∴(x+1)(x﹣3)=0
则x+1=0或x﹣3=0,
解得x1=﹣1(舍去,不合题意),x2=3.
(3)∵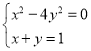 ,
,
∴![]() 或
或![]() ,
,
解得![]() ,
,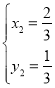 .
.
故答案为![]() ,
,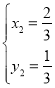 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
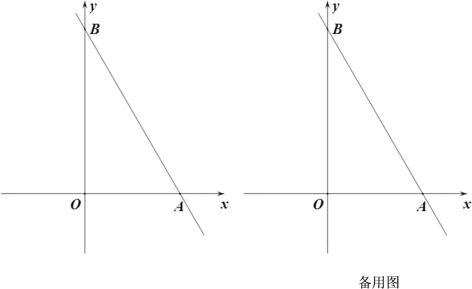
【题目】如图,在平面直角坐标系xOy中,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() 、交
、交![]() 轴于点
轴于点![]() ,
,
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)设点![]() 是
是![]() 轴上的一点
轴上的一点
①在坐标平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,求出
为顶点的四边形是菱形?若存在,求出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
②若![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的x,y的对应值如下表:

下列关于该函数性质的判断
①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
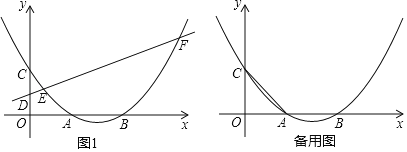
【题目】抛物线y=![]() x2﹣3mx+2m+1与x轴正半轴交于A,B两点(A在B的左侧),与y轴正半轴交于点C,且OA=OC.
x2﹣3mx+2m+1与x轴正半轴交于A,B两点(A在B的左侧),与y轴正半轴交于点C,且OA=OC.
(1)抛物线的解析式为 (直接写出结果);
(2)如图1,D为y轴上一点,过点D的直线y=![]() x+n交抛物线于E,F,若EF=5
x+n交抛物线于E,F,若EF=5![]() ,求点D的坐标;
,求点D的坐标;
(3)将△AOC绕平面内某点逆时针旋转90°至△A'O'C'(点A,C,O的对应点分别为A',C',O'),若旋转后的△A'O'C'恰好有一边的两个端点落在抛物线上,请求出点A'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
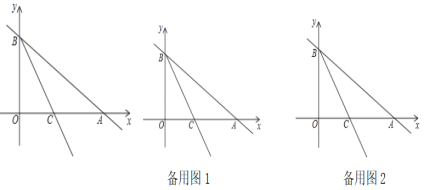
【题目】如图,已知![]() 、
、![]() 两点是直线
两点是直线![]() 与
与![]() 轴的正半轴,
轴的正半轴,![]() 轴的正半轴的交点,如果
轴的正半轴的交点,如果![]() ,
,![]() 的长分别是x2-14x+48=0的两个根
的长分别是x2-14x+48=0的两个根![]() ,射线
,射线![]() 平分
平分![]() 交
交![]() 轴于
轴于![]() 点,
点,
(1)求![]() ,
,![]() 的长.
的长.
(2)求点![]() 的坐标.
的坐标.
(3)在坐标平面内找点![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点的四边形是平行四边形?若存在,请直接写出点
四个点为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
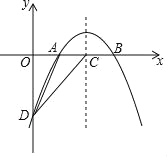
【题目】如图,已知二次函数y=﹣![]() x2+bx+c的图象与x轴交于A、B两点,与y轴交于D点,其中B(6,0),D(0,﹣6)
x2+bx+c的图象与x轴交于A、B两点,与y轴交于D点,其中B(6,0),D(0,﹣6)
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连结DA、DC,求△ADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小正方形构成的网格中,每个小正方形的顶点叫做格点.
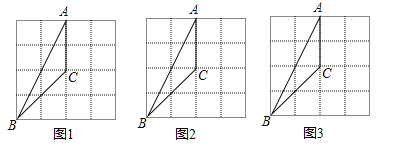
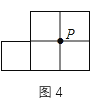
(1)![]() 的三个顶点都在格点上.
的三个顶点都在格点上.
①在图1中,画出一个与![]() 成中心对称的格点三角形;
成中心对称的格点三角形;
②在图2中,画出一个与![]() 成轴对称且与
成轴对称且与![]() 有公共边的格点三角形;
有公共边的格点三角形;
③在图3中,画出![]() 绕着点
绕着点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后的三角形.
后的三角形.
(2)如图4是由5个边长为1的小正方形拼成的图形,请选择适当的格点,用无刻度的直尺面经过点![]() 的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com