练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．一元一次方程1=2x-1的解是（　　）
    A．x=-1B．x=0C．x=1D．x=2

    分析 方程移项合并，把x系数化为1，即可求出解．

    解答 解：方程1=2x-1，
    移项合并得：2x=2，
    解得：x=1．
    故选C．

    点评 此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．有一项工程，由甲、乙两个工程队合作完成，工作一段时间后，乙队改进了技术，提高了工作效率．设甲的工作量为y甲（米），乙的工作量为y乙（米），甲、乙合作完成的工作量为y（米），工作时间为x（时）．y甲与x之间的部分函数图象如图①所示，y与x之间的部分函数图象如图②所示．
    （1）则乙队2天、6天的工作量分别为40；160．
    （2）当2≤x≤6时，求y乙与x的函数关系式；当0≤x≤6时，在图①中画出y乙与x之间的函数图象．
    （3）工作第4天时，甲、乙两队共完成的工作量为200米．
    （4）若6天后，乙保持第6天的工作效率，甲改进了技术，提高了工作效率，当x=8时，甲乙之间的工作量相差10米，求甲提高工作效率后平均每天完成多少米？

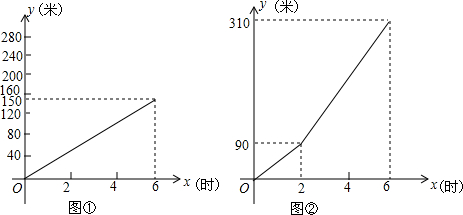
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{|x|=2}\\{2x+y=3}\end{array}\right.$的解，则a+b等于（　　）
    A．1B．5C．1或5D．0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

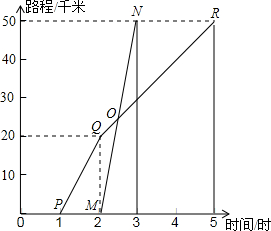    2．如图所示，A、B两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同日下午骑摩托车按同路从A地出发驶往B地，如图所示，图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系．
    根据图象回答下列问题：
    （1）甲和乙哪一个出发更早？早出发多长时间？
    （2）甲和乙哪一个更早到达B城，早多长时间？
    （3）求出乙出发多长时间就追上甲？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．为了加强公民的节水意识，合理利用水资源，各地采用价格调控手段达到节约用水的目的．某市规定如下用水收费标准：每户每月的用水量不超过6立方米时，水费按每立方米a元收费，超过6立方米时，不超过的部分，每立方米仍按a元收费，超过的部分，每立方米按c元收费，该市某户今年四五月份的用水量和所交水费如下表所示：涉牧户每月用水量x立方厘米，应交水费y元．
    为了加强公民的节水意识，合理利用水资源，各地采用价格调控等手段达到节约用水的目的．某市规定如下用水收费标准：每户每月的用水不超过6立方米时，水费按每立方米a元收费；超过6立方米时，不超过的部分每立方米仍按a元收费，超过的部分每立方米按c元收费．该市某户今年4，5月份的用水量和水费如下表所示：
    月份用水量（m3）收费（元）
    357.5
    4927
    设某户该月用水量为x（立方米），应交水费y（元）．
    （1）求a，c的值；
    （2）当x≤6，x≥6时，分别写出y于x的函数关系式；
    （3）若该户6月份的用水量为8立方米，求该户6月份的水费是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

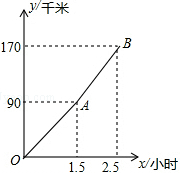    19．“五一节”期间，张老师一家自驾游去了离家170千米的某地，下面他们一家离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象．
    （1）分别求出0≤x≤1.5和1.5＜x≤2.5时的函数解析式；
    （2）出发1.5小时内，汽车的平均行驶速度是多少？
    （3）当张老师一家离目的地还有20千米时，汽车一共行驶的时间是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

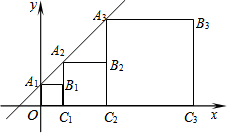    6．如图，正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…，AnBnCnCn-1按所示的方式放置．点A1，A2，A3，…，An和点C1，C2，C3，…，Cn分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则点B2015的坐标是（22015-1，22014）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．己知函数y=$（k-2）{x^{{k^2}-5}}$为反比例函数．
    （1）求k的值；
    （2）它的图象在第二、四象限内，在各象限内，y随x增大而增大；（填变化情况）
    （3）求出-2≤x≤-$\frac{1}{2}$时，y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．
    （1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是DE+DF=AD；
    （2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=$\frac{1}{2}$AD，请给出证明；
    （3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．

    查看答案和解析>>

    同步练习册答案