
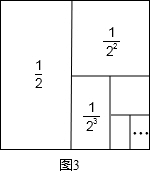

| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
| 5 |
| 6 |
| 11 |
| 12 |
| 23 |
| 24 |
| 47 |
| 48 |
| 95 |
| 96 |
| 191 |
| 192 |
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
| 99×100 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 5 |
| 6 |
| 11 |
| 12 |
| 23 |
| 24 |
| 47 |
| 48 |
| 95 |
| 96 |
| 191 |
| 192 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 24 |
| 1 |
| 48 |
| 1 |
| 96 |
| 1 |
| 192 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 26 |
| 1 |
| 3 |
| 1 |
| 26 |
| 363 |
| 64 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
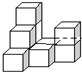 18、如图,是由若干个完全相同的小正方体组成的一个几何体.
18、如图,是由若干个完全相同的小正方体组成的一个几何体.
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 层数 | 1 | 2 | 3 | … | n |
| 每层圆圈个数 | … |
| n(n+3) |
| 2 |
| n(n+3) |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
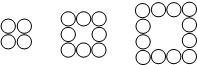 2008年奥运期间,小区物业用花盆妆点院落.下列的每一个图都是由若干个花盆组成的正方形图案.
2008年奥运期间,小区物业用花盆妆点院落.下列的每一个图都是由若干个花盆组成的正方形图案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com