
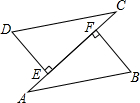
 如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.
如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.分析 认真审题可以发现,题目提供的条件是两个三角形都是直角三角形,而且知道,这两个直角三角形的一条直角边和一条斜边分别相等,所以可以根据“HL”定理判定这两个直角三角形全等,然后得出EC=FA,据此对甲、乙两个学生的解答思路进行分析即可.
解答 解:∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°,
在Rt△DEC和Rt△BFA中,
$\left\{\begin{array}{l}{DC=BA}\\{DE=BF}\end{array}\right.$,
∴Rt△DEC≌Rt△BFA(HL),
∴EC=FA,
∴EC-EF=AF-EF,
即CF=AE,
由上可知,学生乙的解答过程正确,
学生甲的解答过程错误,
错误有两个,
①在Rt△ABF与Rt△CDE中,$\left\{\begin{array}{l}{AB=CD}\\{DE=BF}\end{array}\right.$应改为$\left\{\begin{array}{l}{AB=CD}\\{BF=DE}\end{array}\right.$,
②由Rt△ABF≌Rt△CDE得到的直接结果是:EC=FA.
点评 本题主要考查了直角三角形的判定定理,即:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等,注意总结.


科目:初中数学 来源: 题型:选择题
| A. | x=±2 | B. | $x=±\frac{1}{2}$ | C. | x=±2或x=±$\frac{1}{2}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察下列每对数在数轴上的对应点间的距离:4与7,3与-5,-2与-5,0与-3
观察下列每对数在数轴上的对应点间的距离:4与7,3与-5,-2与-5,0与-3查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com