Question

2．已知在平行四边形ABCD中，AE⊥BC于E点，DF平分∠ADC 交线段AE于F点．
（1）如图1，若AE=AD，求证：CD=AF+BE；
（2）如图2，若AE：AD=a：b，试探究线段CD、AF、BE之间所满足的等量关系，请直接写出你的结论．

Answer 1

分析 （1）延长EA到G，使得AG=BE，连接DG，根据四边形ABCD是平行四边形，推出AB=CD，AB∥CD，AD=BC，求出∠DAG=90°=∠GAD，根据SAS证△ABE≌△DAG，推出DG=AB=CD，∠1=∠2，求出∠AFD=∠GDF，推出DG=GF=AF+AG即可；
（2）延长EA到G，使得$\frac{BE}{AG}$=$\frac{a}{b}$，连接DG，根据两边对应成比例，且夹角相等，两三角形相似，推出△ABE∽△DGA，推出∠1=∠2，DG=AB，代入即可求出答案．

解答 解：（1）证明：延长EA到G，使得AG=BE，连接DG，
∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，AD=BC，
∵AE⊥BC于点E，
∴∠AEB=∠AEC=90°，
∴∠AEB=∠DAG=90°，
∴∠DAG=90°，
在△ABE和△DGA中
$\left\{\begin{array}{l}{BE=GA}\\{∠GAD=∠BEA}\\{AE=AD}\end{array}\right.$，
∴△ABE≌△DGA，
∴∠1=∠2，DG=AB，∠B=∠G，
∵四边形ABCD是平行四边形，
∴∠B=∠ADC，
∵∠B+∠1=∠ADC+∠2=90°，∠3=∠4，
∴∠GDF=90°-∠4，∠GFD=90°-∠3，
∴∠GDF=∠GFD，
∴GF=GD=AB=CD，
∵GF=AF+AG=AF+BE，
∴CD=AF+BE；

（2）bCD=aAF+bBE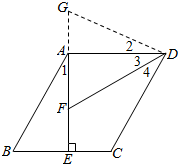
理由是：延长EA到G，使得$\frac{BE}{AG}$=$\frac{a}{b}$，连接DG，
即AG=$\frac{b}{a}$BE，
∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，AD=BC，
∵AE⊥BC于点E，
∴∠AEB=∠AEC=90°，
∴∠AEB=∠DAG=90°，
∴∠DAG=90°，
即∠AEB=∠GAD=90°，
∵$\frac{AE}{AD}$=$\frac{BE}{AG}$=$\frac{a}{b}$，
∴△ABE∽△DGA，
∴∠1=∠2，$\frac{AB}{DG}$=$\frac{a}{b}$，
∴∠GFD=90°-∠3，
∵DF平分∠ADC，
∴∠3=∠4，
∴∠GDF=∠2+∠3=∠1+∠4=180°-∠FAD-∠3=90°-∠3．
∴∠GDF=∠GFD，
∴DG=GF，
∵$\frac{AB}{DG}$=$\frac{a}{b}$，AB=CD（已证），
∴bCD=aDG=a（$\frac{b}{a}$BE+AF），
即 bCD=aAF+bBE．

点评 本题综合考查了全等三角形的性质和判定，相似三角形的性质和判定，角平分线定义，平行线的性质，平行四边形的性质等知识点的运用，本题综合性比较强，有一定的难度，但主要考查学生的类比推理的思想，主要检查学生能否找出解题思路，注意：解题思路的相似之处啊．