
����Ŀ����1���������ֲ�ͬ�ķ����д���ʽ��ʾͼ1�����
����1 ��
����2 ��
��2����a+b=7��ab=15�����ݣ�1���Ľ�����a2+b2��ֵ��
��3����ͼ2�����߳�Ϊx��x+2�ij����Σ��ֳɱ߳�Ϊx�������κ�������Ϊ1��С�����Σ�����������ͼ��ƴ��ͼ3����ʱֻ��Ҫ��һ���߳�Ϊ1�������α���Թ���һ���������Σ�
����һ�������ε������216���ҳ��ȿ���6������������εĿ���
�ڰ�һ����Ϊm����Ϊn�ij����Σ�m��n��������������ƴ��һ����һ��ȥ��һ��С�����εĴ������Σ���ȥ����С�����εı߳�Ϊ ��

���𰸡���1������������2��19����3����12����![]() .
.
��������
��1��ͼ1�ɿ����DZ߳�Ϊ��a+b���������������Ҳ�ɿ����߳��ֱ�Ϊa��b��2���������������2����Ϊa��Ϊb�ľ��������
��2�����ݣ�1���ɵù���a��b�ĵ�ʽ������֪��ֵ������м��㼴�ɵô� ��
��3����ͼ2��ͼ3��֪������ԭ�����εij�Ϊm����Ϊn����ƴ�ɵĴ������εı߳�Ϊ(n+![]() )�����½�С�����α߳�Ϊ
)�����½�С�����α߳�Ϊ![]() ��
��
��1������1��ͼ1�ɿ����DZ߳�Ϊ��a+b�������������������a+b��2
����2��ͼ1�ɿ����DZ߳��ֱ�Ϊa��b��2���������������2����Ϊa��Ϊb�ľ����������a2+2ab+b2
�ʴ�Ϊ����a+b��2��a2+2ab+b2
��2����a+b=7
�ࣨa+b��2=49����a2+2ab+b2=49
�֡�ab=15
��a2+b2=49-2ab=19
�ʴ�Ϊ��19
��3�������Ϊx��������ɵã�
��x+6��2��2=216+��6��2��2
��Ϊx��0�����x=12��
�ʴ�Ϊ��12
�������֪��ȥ��С�����εı߳���ԭ�����γ�������һ��.
�ʴ�Ϊ��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ҹ��ϱ���ʱ�ڣ�Լ��Ԫ5���ͣ���������ѧ�ң����С������㾭����һ������ϣ�������һ���⣺������һֻ¹�����ܣ���������![]() ��ʱ����¹���ڵ�
��ʱ����¹���ڵ�![]() ������36�����Ŵ���1��=300������¹ͻȻ���ܣ���ʱ���������˾�����
������36�����Ŵ���1��=300������¹ͻȻ���ܣ���ʱ���������˾�����![]() ȥ����50����
ȥ����50����![]() ����¹���ڵ�λ��
����¹���ڵ�λ��![]() ������10������
������10������![]() ��
��![]() ��
��![]() ��ͬһֱ���ϣ��������¹����ת�������������ܣ�������Ҫ��Զ�����ϴ�¹��������֪��λʱ����¹�ܵ�·�̺����������ϵ�·�̵ı�ֵ�Ƕ�ֵ������������⣮
��ͬһֱ���ϣ��������¹����ת�������������ܣ�������Ҫ��Զ�����ϴ�¹��������֪��λʱ����¹�ܵ�·�̺����������ϵ�·�̵ı�ֵ�Ƕ�ֵ������������⣮


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ2�ĵȱ�������ABC�Ķ���C��ֱ��l�� BC��Ȼ������ABC����ֱ��l�ԳƵġ�A��B��C��PΪ�߶�A��C��һ���㣬����AP��PB����AP��PB����Сֵ�� �� ��
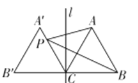
A.4B.3C.2D.2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B������ֱ�Ϊ��1�� 4���ͣ�4�� 4����������![]() �Ķ������߶�AB���˶�����x�ύ��C��D���㣨C��D����ࣩ����C�ĺ�������СֵΪ-3�����D�ĺ��������ֵΪ_______��
�Ķ������߶�AB���˶�����x�ύ��C��D���㣨C��D����ࣩ����C�ĺ�������СֵΪ-3�����D�ĺ��������ֵΪ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����![]() ����
����![]() .����˵���У���ȷ�ĸ����ǣ� ��
.����˵���У���ȷ�ĸ����ǣ� ��
��![]() �� �����
�� �����![]() ����ô
����ô![]() ����
����![]() �� ��
�� ��![]()
A. ![]() ��B.
��B. ![]() ��C.
��C. ![]() ��D.
��D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������A��B��C�����ǿ����������������ƶ�����ش�
��1����A��B��C�ֱ��ʾ������______________________��
��2������B �����ƶ�������λ���Ⱥ��D����D��ʾ������_____________��
��3���ƶ���A�����E��ʹB��C��E�������������һ��Ϊ������������֮���߶ε��е㣬��ֱ��д�����е�A �ƶ��ľ���ͷ���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ţ��ij��O��ʼ�ض�������ֱ�����У��涨�����е�·�̼�Ϊ�������������е�·�̼�Ϊ���������еĸ���·������Ϊ����λ�����ף���![]() .�ʣ�
.�ʣ�
��1����ţ����Ƿ�ص�������O��
��2����ţ�뿪������O��Զ�Ƕ������ף�
��3�������й����У����ÿ����1������һ��֥�飬����ţ�ɵõ�������֥�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AE��һ���㣨�����A��E�غϣ�����AEͬ��ֱ�������ABC������CDE��AD��BE���ڵ�O��AD��BC���ڵ�P��BE��CD���ڵ�Q������PQ������������ۣ���AD=BE����PQ��AE����AP=BQ����DE=DP���ݡ�AOB=60����
������Ľ����� ����������Ϊ��ȷ����Ŷ����ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=x2��4x+4��y������ƽ��9����λ����������������x�������ύ�ڵ�B����y�ύ�ڵ�C������ΪD����1����B��C��D���ꣻ��2����BCD�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com