
 四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?
四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?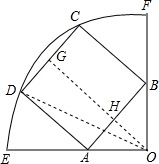 解:过点O作OG⊥CD于点G,交AB于点H,连接OD,
解:过点O作OG⊥CD于点G,交AB于点H,连接OD,| 10 |
| 10 |


科目:初中数学 来源: 题型:
 在平行四边形ABCD中,AE⊥BC于E,CF⊥AD于F,AE交BF于M,CF交DE于N.
在平行四边形ABCD中,AE⊥BC于E,CF⊥AD于F,AE交BF于M,CF交DE于N.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 合肥市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为48m,这栋高楼有多高?(结果精确到1m,参考数据:
合肥市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为48m,这栋高楼有多高?(结果精确到1m,参考数据:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com