
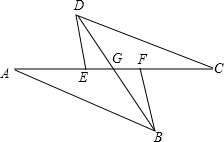
 已知:AB=CD,AF=CE,DE⊥AC,BF⊥AC,BD与AC交于点G.求证:EG=FG.
已知:AB=CD,AF=CE,DE⊥AC,BF⊥AC,BD与AC交于点G.求证:EG=FG. 分析 先证明Rt△AFB≌Rt△CED,得到DE=BF,再证明△DEG≌△BFG,即可得到EG=FG.
解答 解:∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
在Rt△AFB和Rt△CED中,
$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$
∴Rt△AFB≌Rt△CED,
∴DE=BF,
在△DEG和△BFG中,
$\left\{\begin{array}{l}{∠DEC=∠BFA}\\{∠DGE=∠BGF}\\{DE=BF}\end{array}\right.$
∴△DEG≌△BFG,
∴EG=FG.
点评 本题考查了全等三角形的判定定理和性质定理,解决本题的关键是证明Rt△AFB≌Rt△CED,△DEG≌△BFG.


科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABE≌△ACD,且AB=AC.
如图所示,已知△ABE≌△ACD,且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:选择题
为执行“均衡教育”政策,某县2014年投入教育经费2500万元,预计到2016年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长 百分率为x,则下列方程正确的是( )
A.2500(1+x)2=1.2
B.2500(1+x)2=12000
C.2500+2500(1+x)+2500(1+x)2=1.2
D.2500+2500(1+x)+2500(1+x)2=12000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com