
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� �����йصĶ����Ͷ��������жϼ��ɵõ��𰸣�
��� �⣺�ٸ��������$\left\{\begin{array}{l}{2-2x��0}\\{{x}^{2}-x��0}\end{array}\right.$����x��ȡֵ��ΧΪx��1��x��0��ԭ�������
��3235.97��Ԫ��3.2360��1011Ԫ���ʴ���
�۸��ݷ���������y=$\frac{m}{x}$��mΪ�������������Եó�m��0����һ�κ���y=-2x+m��ͼ��һ����������һ���ޣ�
��ѡ����ȷ��
����������ͼ�����y��Գƣ�������Ϊż������������������y=3��y=x2��ż������ԭ�������
��ѡB��
���� ���⿼���������붨����֪ʶ�����ж� һ�����������ʱ����Ծٳ�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��Բ���ܳ�Ϊ4����λ���ȣ��ڸ�Բ��4�ȷֵ㴦�ֱ����0��1��2��3������Բ���ϱ�ʾ����0�ĵ��������ϱ�ʾ-1�ĵ��غϣ��ٽ����ᰴ��ʱ�뷽�����ڸ�Բ�ϣ��������ϱ�ʾ2015�ĵ���Բ���ϱ�ʾ�����ĸ����غϣ���������
��ͼ��Բ���ܳ�Ϊ4����λ���ȣ��ڸ�Բ��4�ȷֵ㴦�ֱ����0��1��2��3������Բ���ϱ�ʾ����0�ĵ��������ϱ�ʾ-1�ĵ��غϣ��ٽ����ᰴ��ʱ�뷽�����ڸ�Բ�ϣ��������ϱ�ʾ2015�ĵ���Բ���ϱ�ʾ�����ĸ����غϣ���������| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
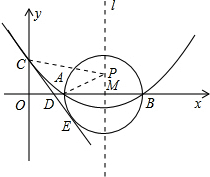 ��ͼ����֪������y=ax2+bx+c��a��0����x�ύ��A��2��0����B��6��0�����㣬����y�ύ�ڵ�C��0��2����
��ͼ����֪������y=ax2+bx+c��a��0����x�ύ��A��2��0����B��6��0�����㣬����y�ύ�ڵ�C��0��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
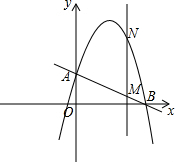 ��ͼ��һ�κ���y=-$\frac{1}{2}$x+2�ֱ�y�ᡢx����A��B���㣬������y=-x2+bx+c��A��B���㣮
��ͼ��һ�κ���y=-$\frac{1}{2}$x+2�ֱ�y�ᡢx����A��B���㣬������y=-x2+bx+c��A��B���㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com