
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.

【答案】(1)菱形;(2)证明见解析;(3)![]()
【解析】(1)根据菱形的判定方法进行判定即可.
![]() 根据正方形的判定方法进行判定即可.
根据正方形的判定方法进行判定即可.
![]() 在Rt△ABC中,根据sin∠ACB=
在Rt△ABC中,根据sin∠ACB=![]() ,求出∠ACB=30°,在Rt△BCH中,求出
,求出∠ACB=30°,在Rt△BCH中,求出![]() 在Rt△ABH中,求出
在Rt△ABH中,求出![]() 的长度,根据锐角三角函数的定义求解即可.
的长度,根据锐角三角函数的定义求解即可.
(1)在如图1中,
∵AC是矩形ABCD的对角线,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠BAC,
在如图2中,由旋转知,AC'=AC,∠AC'D=∠ACD,
∴∠BAC=∠AC'D,
∵∠CAC'=∠BAC,
∴∠CAC'=∠AC'D,
∴AC∥C'E,
∵AC'∥CE,
∴四边形ACEC'是平行四边形,
∵AC=AC',
∴ACEC'是菱形,
故答案为:菱形;
(2)在图1中,∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAD=∠ACB,∠B=90°,
∴∠BAC+∠ACB=90°,
在图3中,由旋转知,∠DAC'=∠DAC,
∴∠ACB=∠DAC',
∴∠BAC+∠DAC'=90°,
∵点D,A,B在同一条直线上,
∴∠CAC'=90°,
由旋转知,AC=AC',
∵点F是CC'的中点,
∴AG⊥CC',CF=C'F,
∵AF=FG,
∴四边形ACGC'是平行四边形,
∵AG⊥CC',
∴ACGC'是菱形,
∵∠CAC'=90°,
∴菱形ACGC'是正方形;
(3)在Rt△ABC中,AB=2,AC=4,
∴BC'=AC=4,BD=BC=2![]() ,sin∠ACB=
,sin∠ACB=![]() ,
,
∴∠ACB=30°,
由(2)结合平移知,∠CHC'=90°,
在Rt△BCH中,∠ACB=30°,
∴BH=BCsin30°=![]() ,
,
∴![]()
在Rt△ABH中,AH=![]() AB=1,
AB=1,
∴CH=AC-AH=4-1=3,
在Rt△CHC'中,tan∠C′CH=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )

A. ①②③ B. ①③④ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电力维修小组从![]() 点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
(1)求收工时在![]() 地的什么方位?
地的什么方位?
(2)在记录中,距离![]() 最远有 千米?
最远有 千米?
(3)若每千米耗油0.2升,油价为5元/升,问出发到收工时共需要多少元油钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
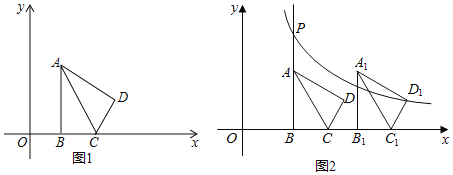
【题目】如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=![]() (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
(k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图:已知D为等腰直角△ABC斜边BC上的一个动点(D与B、C均不重合),连结AD,△ADE是等腰直角三角形,DE为斜边,连结CE,求∠ECD的度数.
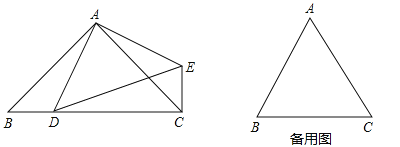
(2)当(1)中△ABC、△ADE都改为等边三角形,D点为△ABC中BC边上的一个动点(D与B、C均不重合),当点D运动到什么位置时,△DCE的周长最小?请探求点D的位置,试说明理由,并求出此时∠EDC的度数.
(3)在(2)的条件下,当点D运动到使△DCE的周长最小时,点M是此时射线AD上的一个动点,以CM为边,在直线CM的下方画等边三角形CMN,若△ABC的边长为4,请直接写出DN长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
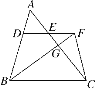
【题目】已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,连接BF,交边AC于点G,连接CF.
(1)求证:![]() ;
;
(2)如果CF2=FG·FB,求证:CG·CE=BC·DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店5月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.6月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店6月份购进这两种水果的数量与5月份都相同,将多支付货款300元,求该店5月份购进甲、乙两种水果分别是多少千克?
(2)若6月份将这两种水果进货总量减少到120千克,且甲种水果不超过乙种水果的3倍,则6月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com