
| A. | y=(x-23)2+155 | B. | y=(x+23)2+155 | C. | y=-(x-23)2-155 | D. | y=-(x+23)2+155 |
分析 根据顶点坐标和开口方向依次做判断即可.
解答 解:A、顶点为(23,155),在第一象限,且开口向上,所以与x轴无交点;
B、顶点为(-23,155),在第二象限,且开口向上,所以与x轴无交点;
C、顶点为(23,-155),在第四象限,且开口向下,所以与x轴无交点;
D、顶点为(-23,155),在第二象限,且开口向下,所以与x轴有两个交点;
本题选择与x轴有两个交点的二次函数的图象,
故选D.
点评 本题考查了抛物线与x轴的交点个数问题,有两种方法来判断:①把二次函数化为一般形式,计算b2-4ac的值,根据△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.②二次函数为顶点式时,根据顶点坐标位置和开口方向,利用数形结合做判断;本题就是采取第②种方法进行解答的.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{4}$ | C. | 0 | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
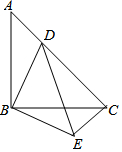 等腰Rt△ABC中,BA=BC,∠ABC=90°,将△ABD绕点B顺时针旋转90°后,得到△CBE.若AB=6,CD=2AD,求DE的长.
等腰Rt△ABC中,BA=BC,∠ABC=90°,将△ABD绕点B顺时针旋转90°后,得到△CBE.若AB=6,CD=2AD,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
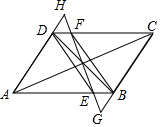 如图,已知?ABCD的对角线AC与BD相交于点O,过点O的直线与AB,DC分别交于点E,F
如图,已知?ABCD的对角线AC与BD相交于点O,过点O的直线与AB,DC分别交于点E,F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com