
如图,点O是边长为8的正方形ABCD边AD上一个动点(4<OA<8),以O为圆心、OA长为半径的圆交边CD于点M,连接OM,以CM为边在正方形ABCD内部作∠CMN=∠DOM,直线MN交边BC于点N.
(1)试说明:直线MN是⊙O的切线;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你有什么发现?
(1)根据正方形的性质结合∠CMN=∠DOM,即可得到∠OMN=90°,即可证得结果;
(2)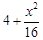 ;(3)p为定值16
;(3)p为定值16
解析试题分析:(1)根据正方形的性质结合∠CMN=∠DOM,即可得到∠OMN=90°,即可证得结果;
(2)设OA=y,Rt△ODM中,根据勾股定理可得DM2=OM2-DO2=OA2-DO2,即可得到结果;
(3)易证△DOM ∽△CMN,根据相似三角形的性质可得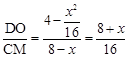 ,即可得到结果.
,即可得到结果.
(1)∵正方形ABCD
∴∠D=90°
∴∠DOM+∠DMO=90°
∵∠CMN=∠DOM
∴∠CMN+∠DMO=90°
∴∠OMN=90°
∴直线MN是⊙O的切线;
(2)设OA=y,Rt△ODM中,DM2=OM2-DO2=OA2-DO2,
即x2=y2-(8-y)2,解得OA=y =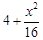 ;
;
(3)易证△DOM ∽△CMN,相似比为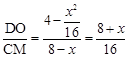 ,
,
∴p=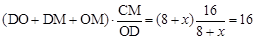 .
.
∴在点O运动的过程中,△CMN的周长p为定值16.
考点:函数的应用
点评:此类问题综合性强,难度较大,在中考中比较常见,题目比较典型.


科目:初中数学 来源: 题型:
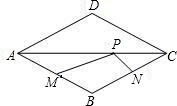 如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别为AB,BC边上的中点,则MP+NP的最小值是( )
如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别为AB,BC边上的中点,则MP+NP的最小值是( )| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
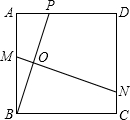 垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.
垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.查看答案和解析>>
科目:初中数学 来源: 题型:
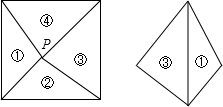
 如图.点P是边长为1的正方形ABCD对角线AC上的一个动点(P不与A,C重合)且PE=PB
如图.点P是边长为1的正方形ABCD对角线AC上的一个动点(P不与A,C重合)且PE=PB 查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com