
| 甲 | 乙 | |
| 价格(万元/1台) | 7 | 5 |
| 每台日产量(个) | 100 | 60 |
分析 (1)根据题意可知y=2x+30,利用“甲种机器购买的台数不能少于总台数的一半”“购买机器所耗资金不能超过40万元”可得到3≤x≤5,因为x为整数,∴x=2,3,4,5,故有,四种购买方案;
(2)根据“日生产能力不能低于500个”可得100x+60(6-x)≥500,即得到x=4或5,y随x的增大而增大,考虑节约资金,应取x=4时的方案;
(3)根据题意列方程即可得到结论.
解答 解:(1)y与x之间的函数关系式为:y=7x+5(6-x)=2x+30,
∵甲种机器购买的台数不能少于乙种机器台数的一半且购买机器所耗资金不能超过40万元,
∴x≥$\frac{1}{2}(6-x)$,2x+30≤40,
∴2≤x≤5,
∵x为整数,
∴x=2,3,4,5,
故有四种购买方案:甲2台乙4台;甲3台乙3台;甲4台乙2台;甲5台乙1台,
(2)根据题意得:100x+60(6-x)≥500,
解得:x≥3.5,
∴x=4,5,
∵k=2>0,
∴y随x的增大而增大,
∴考虑节约资金,应取x=4时的方案,
∴当甲4台乙2台时,所用资金最少为38万元.
(3)设a天可回收投资且盈利100万元.
根据题意得(60×4×100+60×2×50-22000)a=100+38,
∴a=172.5天,
∴172.5天可回收投资且盈利100万元.
点评 本题考查了一次函数的应用,一元一次不等式的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式,正确确定各种情况,确定各种方案是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点G,过D作EF⊥AC于点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点G,过D作EF⊥AC于点E,交AB的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
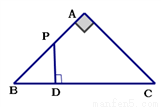
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. 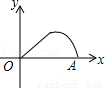 B.
B.  C.
C. 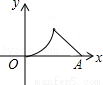 D.
D. 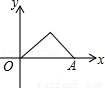
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com