
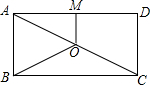
 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9. 分析 根据题意可知OM是△ADC的中位线,所以OM的长可求;根据勾股定理可求出AC的长,利用直角三角形斜边上的中线等于斜边的一半可求出BO的长,进而求出四边形ABOM的周长.
解答 解:∵O是矩形ABCD的对角线AC的中点,M是AD的中点,
∴OM=$\frac{1}{2}$CD=$\frac{1}{2}$AB=1.5,
∵AB=3,AD=4,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵O是矩形ABCD的对角线AC的中点,
∴BO=$\frac{1}{2}$AC=2.5,
∴四边形ABOM的周长为AB+AM+BO+OM=3+2+2.5+1.5=9,
故答案为:9.
点评 本题考查了矩形的性质、三角形的中位线的性质以及直角三角形斜边上的中线等于斜边的一半这一性质,题目的综合性很好,难度不大.


科目:初中数学 来源: 题型:选择题
| A. | -2x+3x=x | B. | 2xy2•(-x)=-2x2y2 | C. | (-2x2y)3=-6x2y3 | D. | 6xy2÷2xy=3y |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全等三角形的对应角相等 | |
| B. | 如果两个数相等,那么它们的绝对值相等 | |
| C. | 对角线互相平分的四边形是平行四边形 | |
| D. | 如果两个角都是90°,那么这两个角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,E为BC边上一点,且AB=AE.
如图,?ABCD中,E为BC边上一点,且AB=AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{5}{2}$ | B. | x>6 | C. | x$<\frac{5}{2}$ | D. | $\frac{5}{2}<x<6$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com