
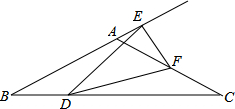
 已知:如图,在△ABC中,AB=AC,BC为最大边,点D、F分别在BC、AC上.BD=CF,E为BA延长线上一点.若∠B=∠EDF=∠C=30°,求∠DEF的度数.
已知:如图,在△ABC中,AB=AC,BC为最大边,点D、F分别在BC、AC上.BD=CF,E为BA延长线上一点.若∠B=∠EDF=∠C=30°,求∠DEF的度数.
|
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 在任意三角形ABC边上画正方形ABDE、ACGF,连接BE、FC、EF,并取BE、FC、EF、BC的中点I、J、H、K,连接IH、HJ、JK、IK,求证:HIKJ为正方形.
在任意三角形ABC边上画正方形ABDE、ACGF,连接BE、FC、EF,并取BE、FC、EF、BC的中点I、J、H、K,连接IH、HJ、JK、IK,求证:HIKJ为正方形.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,表示的大刚与爷爷春游时,沿相同的路线同时从山脚下出发到达山顶的过程中,各自行进的路程随时间变化的图象.请你根据图象提供的信息解答下列问题:
如图,表示的大刚与爷爷春游时,沿相同的路线同时从山脚下出发到达山顶的过程中,各自行进的路程随时间变化的图象.请你根据图象提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,均匀的正四面体的各面依次标有1,2,3,4四个数.
如图,均匀的正四面体的各面依次标有1,2,3,4四个数.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com