

分析 (1)依据△ABC是等腰直角三角形,E是BC的中点,运用SAS即可判定△BPE≌△CQE;
(2)依据∠B=∠C=∠DEF=45°,即可得到∠BEP=∠EQC,再根据∠B=∠C,即可判定△BPE∽△CEQ;
(3)先根据△BPE∽△CEQ,得到$\frac{BP}{CE}$=$\frac{BE}{CQ}$,进而得到BE=CE=$\frac{3}{2}\sqrt{2}$,BC=3$\sqrt{2}$,最后根据勾股定理,求得Rt△APQ中,PQ=$\sqrt{A{Q}^{2}+A{P}^{2}}$=$\frac{5}{2}$.
解答  解:(1)△BPE≌△CQE.
解:(1)△BPE≌△CQE.
理由∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,AB=AC,
∵AP=AQ,
∴BP=CQ,
∵E是BC的中点,
∴BE=CE,
在△BPE和△CQE中,
$\left\{\begin{array}{l}{BP=CQ}\\{∠B=∠C}\\{BE=CE}\end{array}\right.$,
∴△BPE≌△CQE(SAS);
(2)△BPE∽△CEQ.
理由:∵△ABC和△DEF是两个全等的等腰直角三角形,
∴∠B=∠C=∠DEF=45°,
∵∠BEQ=∠EQC+∠C,
即∠BEP+∠DEF=∠EQC+∠C,
∴∠BEP+45°=∠EQC+45°,
∴∠BEP=∠EQC,
∵∠B=∠C,
∴△BPE∽△CEQ;
(3)如图②,连结PQ,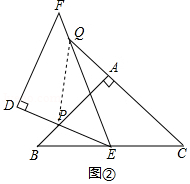
∵△BPE∽△CEQ,
∴$\frac{BP}{CE}$=$\frac{BE}{CQ}$,
∵BP=1,CQ=$\frac{9}{2}$,BE=CE,
∴$\frac{1}{CE}$=$\frac{CE}{\frac{9}{2}}$,
∴BE=CE=$\frac{3}{2}\sqrt{2}$,
∴BC=3$\sqrt{2}$,
在Rt△ABC中,AB=AC,
∴AB=AC=3,
∴AQ=CQ-AC=$\frac{3}{2}$,PA=AB-BP=2,
在Rt△APQ中,PQ=$\sqrt{A{Q}^{2}+A{P}^{2}}$=$\frac{5}{2}$.
点评 本题属于几何变换综合题,主要考查了全等三角形的判定,相似三角形的判定以及勾股定理的综合应用,解决问题的关键是辅助线构造直角三角形,依据相似三角形的对应边成比例,列式计算求得BE,CE的长,并运用勾股定理进行计算.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
| 弹簧总长L/cm | 16 | 17 | 18 | 19 | 20 |
| 重物质量x/千克 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
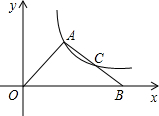 如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )
如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )| A. | 8 | B. | 7.5 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 鞋的尺寸 (单位:厘米) | 23.5 | 24 | 24.5 | 25 | 26 |
| 销售量 (单位:双) | 1 | 2 | 3 | 4 | 2 |
| A. | 25,25 | B. | 24.5,25 | C. | 24.5,24.5 | D. | 25,24.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.
已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com