
【题目】已知:在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上.
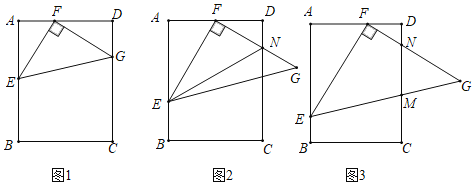
(1)如图1,当点G在CD上时,求证:△AEF≌△DFG;
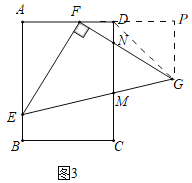
(2)如图2,若F是AD的中点,FG与CD相交于点N,连接EN,求证:EN=AE+DN;
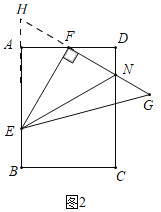
(3)如图3,若AE=AD,EG,FG分别交CD于点M,N,求证:MG2=MNMD.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先用同角的余角相等,判断出∠AEF=∠DFG,即可得出结论;
(2)先判断出△AHF≌△DNF,得出AH=DN,FH=FN,进而判断出EH=EN,即可得出结论;
(3)先判断出AF=PG,PF=AE,进而判断出PG=PD,得出∠MDG=45°,进而得出∠FGE=∠GDM,判断出△MGN∽△MDG,即可得出结论.
(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵∠EFG=90°,
∴∠AFE+∠DFG=90°,
∴∠AEF=∠DFG,
∵EF=FG,
∴△AEF≌△DFG(AAS);
(2)如图2,,
延长NF,EA相交于H,
∴∠AFH=∠DFN,
由(1)知,∠EAF=∠D=90°,
∴∠HAF=∠D=90°,
∵点F是AD的中点,
∴AF=DF,
∴△AHF≌△DNF(ASA),
∴AH=DN,FH=FN,
∵∠EFN=90°,
∴EH=EN,
∵EH=AE+AH=AE+DN,
∴EN=AE+DN;
(3)如图3,
过点G作GP⊥AD交AD的延长线于P,
∴∠P=90°,
同(1)的方法得,△AEF≌△PFG(AAS),
∴AF=PG,PF=AE,
∵AE=AD,
∴PF=AD,
∴AF=PD,
∴PG=PD,
∵∠P=90°,
∴∠PDG=45°,
∴∠MDG=45°,
在Rt△EFG中,EF=FG,
∴∠FGE=45°,
∴∠FGE=∠GDM,
∵∠GMN=∠DMG,
∴△MGN∽△MDG,
∴![]() ,
,
MG2=MNMD.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB与CD都是垂直于地面BC的建筑物.在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°,测得顶端D的仰角为36°,若AC=200米,AD=300米,求建筑物CD的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 都在格点上。
都在格点上。
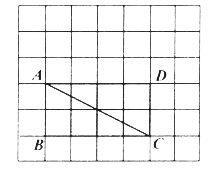
(Ⅰ)AC的长是_____________;
(Ⅱ)将四边形![]() 折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形
折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形![]() .请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点
.请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点![]() 的位置是如何找到的____________________.
的位置是如何找到的____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字![]() ,1,3,6的四张卡片(卡片除数字外,其它都相同)洗匀后,背面向上放在桌子上,从中先随机抽取一张卡片,记下卡片上的数字,不放回,再从中任取一张卡片,记下数字.
,1,3,6的四张卡片(卡片除数字外,其它都相同)洗匀后,背面向上放在桌子上,从中先随机抽取一张卡片,记下卡片上的数字,不放回,再从中任取一张卡片,记下数字.
(1)请用列表或画树状图法(树状图也称树形图)中的一种方法,列出所有可能出现的结果;
(2)请计算两次摸出的卡片上的数字之和大于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某路灯灯架示意图,其中点A表示电灯,AB和BC为灯架,l表示地面,已知AB=2m,BC=5.7m,∠ABC=110°,BC⊥l于点C,求电灯A与地面l的距离.(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
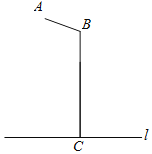
查看答案和解析>>
科目:初中数学 来源: 题型:
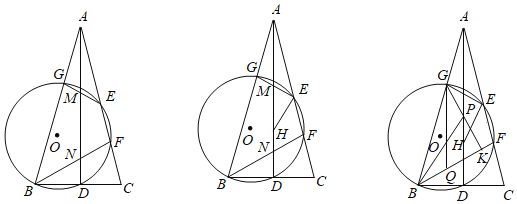
【题目】如图,△ABC中,AB=AC,AD⊥BC于D,E是AC边上一点,⊙O过B、D、E三点,分别交AC、AB于点F、G,连接EG、BF分别与AD交于点M、N;
(1)求证:∠AMG=∠BND;
(2)若点E为AC的中点,求证:BF=BC;
(3)在(2)的条件下,作EH⊥EG交AD于点H,若EH=EG=4![]() ,过点G作GK⊥BF于点K,点P在线段GK上,点Q在线段BK上,连接BP、GQ,若∠KGQ=2∠GBP,GQ=15
,过点G作GK⊥BF于点K,点P在线段GK上,点Q在线段BK上,连接BP、GQ,若∠KGQ=2∠GBP,GQ=15![]() ,求GP的长度.
,求GP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )

A. 33 B. 301 C. 386 D. 571
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com