
【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.

(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)通过证明△ADE≌△CBF,由全等三角的对应边相等证得AE=CF。
(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论。
证明:(1)如图:∵四边形ABCD是平行四边形,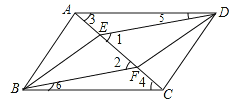
∴AD=BC,AD∥BC,∠3=∠4。
∵∠1=∠3+∠5,∠2=∠4+∠6,
∴∠1=∠2。
∴∠5=∠6。
∵在△ADE与△CBF中,∠3=∠4,AD=BC,∠5=∠6,
∴△ADE≌△CBF(ASA)。
∴AE=CF。
(2)∵∠1=∠2,∴DE∥BF。
又∵由(1)知△ADE≌△CBF,
∴DE=BF。
∴四边形EBFD是平行四边形.
“点睛”本题考查了平行四边形的判定和性质,全等三角形的判定和性质,灵活运用平行四边形的判定定理是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义:如图(1),若分别以△ABC的三边AC、BC、AB为边向三角形外侧作正方形ACDE、BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展
双叶正方形.
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为S1和S2.
①如图(2),当∠ACB=90°时,求证:S1=S2;
②如图(3),当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF、△AEN、△BGM的面积和为S,请利用图(1)探究:当∠ACB的度数发生变化时,S的值是否发生变化?若不变,求出S的值;若变化,求出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某楼盘2013年房价为每平方米8100元,经过两年连续降价后,2015年房价为7600元.设该楼盘这两年房价平均降低率为x,根据题意可列方程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究和应用
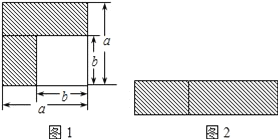
(1)如图1,可以求出阴影部分的面积是__.(写成两数平方差的形式)
(2)如图,若将阴影部分剪下来,重新拼成一个长方形,它的宽是__,长是__,面积是__.(写成多项式乘积的形式)
(3)比较左、右两图阴影部分的面积,可以得到乘法公式__.(用式子来表示)
(4)运用你所得到的公式,计算下列各题.
①![]() ②(2x﹣y+3)(2x﹣3+y)
②(2x﹣y+3)(2x﹣3+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°

(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com