
| A. | 2000名考生是总体的一个样本 | |
| B. | 每个考生是个体 | |
| C. | 这5万名考生的数学中考成绩的全体是总体 | |
| D. | 统计中采用的调查方式是普查 |
分析 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解答 解:A、从中抽取2000名考生的数学成绩是总体的一个样本,故A不符合题意;
B、每个考生的成绩是个体,故B不符合题意;
C、这5万名考生的数学中考成绩的全体是总体,故C符合题意;
D、统计中采取抽样调查,故D不符合题意;
故选:C.
点评 考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
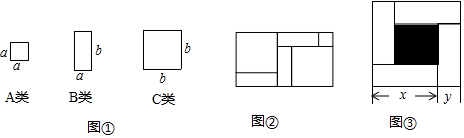
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
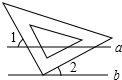 如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2等于( )
如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2等于( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知?ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF=$\sqrt{3}$,EO=1,AE=3,DF=5,S?ABCD=20$\sqrt{3}$.
已知?ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF=$\sqrt{3}$,EO=1,AE=3,DF=5,S?ABCD=20$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
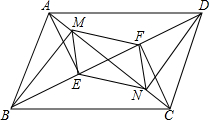 如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.
如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
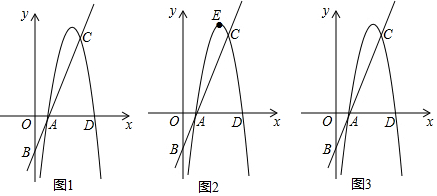
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是59 | B. | 中位数是56 | C. | 众数是82 | D. | 方差是37 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-2x+1=(x-1)2 | B. | ax-ay+a=a(x-y)+a | ||
| C. | x3-x=x(x+1)(x-1)+1 | D. | x2-4+3x=(x+2)(x-2)+3x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com