
【题目】某装修工程,甲、乙两人可以合作完成,若甲、乙两人合作4天后,再由乙独作12天可以完成,已知甲独作每天需要费用580元.乙独作每天需费用280元.但乙单独完成的天数是甲单独完成天数的2倍.
(1)甲、乙两人单独作这项工程各需多少天?
(2)如果工期要求不超过18天完成,应如何安排甲乙两人的工期使这项工程比较省钱?
【答案】
(1)解:设甲单独作这项工程需x天,则乙单独完成需2x天,
根据题意得方程 ( ![]() +
+ ![]() )×4+
)×4+ ![]() =1,
=1,
解得x=12.
经检验x=12是原方程的根.
2x=24
(2)解:设安排甲队施工a天,则乙队施工 ![]() =(24﹣2a)天,设总费用为w元.
=(24﹣2a)天,设总费用为w元.
∵工期不超过18天,
∴ ![]() ,
,
∴3≤a≤18.
W=580a+280(24﹣2a),
整理得w=20a+6720.
∵k=20>0,所以w随a的增大而增大,
当a=3时,w最小,w的值为6780元,24﹣2a=18.
∴当乙队工作18天,同时甲队在此期间工作3天完成这项工程比较省钱
【解析】(1)设甲单独作这项工程需x天,则乙单独完成需2x天,根据甲、乙两人合作4天后,再由乙独作12天可以完成,列出方程,求出方程的解,再进行检验即可;(2)设安排甲队施工a天,则乙队施工 ![]() =(24﹣2a)天,设总费用为w元.根据工期不超过18天,列出关于a的一元一次不等式组
=(24﹣2a)天,设总费用为w元.根据工期不超过18天,列出关于a的一元一次不等式组 ![]() ,解得3≤a≤18.再用含a的代数式表示w,得w=580a+280(24﹣2a),即w=20a+6720.根据一次函数的性质即可求解.
,解得3≤a≤18.再用含a的代数式表示w,得w=580a+280(24﹣2a),即w=20a+6720.根据一次函数的性质即可求解.
【考点精析】关于本题考查的分式方程的应用,需要了解列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:
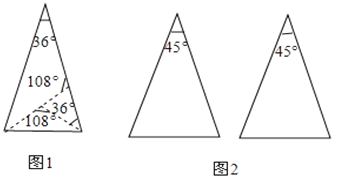
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
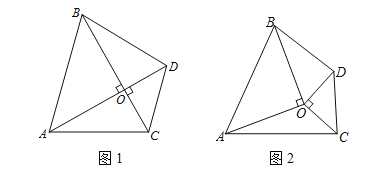
【题目】在△OAB中,OA=OB,OA⊥OB.在△OCD中,OC=OD,OC⊥OD.
(1)如图1,若A,O,D三点在同一条直线上,求证:S△AOC=S△BOD;
(2)如图2,若A,O,D三点不在同一条直线上,△OAB和△OCD不重叠.则S△AOC=S△BOD是否仍成立?若成立,请予以证明;若不成立,也请说明理由.
(3)若A,O,D三点不在同一条直线上,△OAB和△OCD有部分重叠,经过画图猜想,请直接写出 S△AOC和S△BOD的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
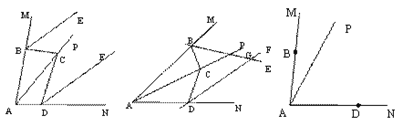
【题目】已知,点B、D分别在∠MAN的两边AM、AN上,点C是射线AP上的一点,连接BC、DC,∠MAN=α,∠BCD=β,(0°<α<180°,0°<β<180°);BE平分∠MBC,DF平分∠NDC.
(1)如图1,若α=β=80°,
①求∠MBC+∠NDC的度数;
②判断BE、DF的位置关系,并说明理由.
(2)如图2,当点C在射线AP上运动时,若直线BE、DF相交于点G,请用含有α、β的代数式表示∠BGD.(直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万美服装店准备购进一批两种不同型号的衣服,已知若购进A型号的衣服9件,B型号的衣服10件共需1 810元;若购进A型号的衣服12件,B型号的衣服8件共需1 880元.已知销售一件A型号的衣服可获利18元,销售一件B型号的衣服可获利30元.
(1)求A、B型号衣服的进价各是多少元?
(2)若已知购进的A型号的衣服比B型号衣服的2倍还多4件,且购进的A型号的衣服不多于28件,则该服装店要想获得的利润不少于699元,在这次进货时可有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
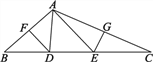
【题目】如图,△ABC中,∠BAC=110°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,BC=10cm.求:
(1)△ADE的周长;
(2)∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
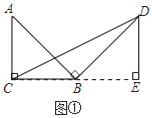
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
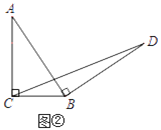
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
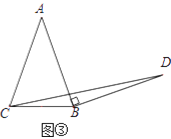
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com