
【题目】如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=![]() ,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
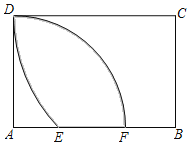
【答案】2π+2﹣4![]()
【解析】
如图,连接EC.首先证明△BEC是等腰直角三角形,根据S阴=S矩形ABCD-(S矩形ABCD-S扇形ADF)-(S矩形ABCD-S扇形CDE-S△EBC)=S扇形ADF+S扇形CDE+S△EBC-S矩形ABCD计算即可.
如图,连接EC.
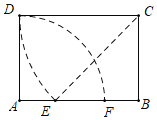
∵四边形ABCD是矩形,
∴AD=BC=2,CD=AB=EC=2![]() ,∠B=∠A=∠DCB=90°,
,∠B=∠A=∠DCB=90°,
∴BE=![]() =
=![]() =2,
=2,
∴BC=BE=2,
∴∠BEC=∠BCE=45°,
∴∠ECD=45°,
∴S阴=S矩形ABCD﹣(S矩形ABCD﹣S扇形ADF)﹣(S矩形ABCD﹣S扇形CDE﹣S△EBC)
=S扇形ADF+S扇形CDE+S△EBC﹣S矩形ABCD
=![]() +
+![]() ×2×2﹣2×2
×2×2﹣2×2![]() ,
,
=2π+2﹣4![]() .
.
故答案为:2π+2﹣4![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
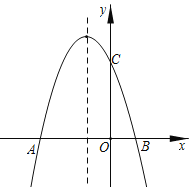
【题目】如图,已知抛物线y=﹣x2+bx+3的对称轴为直线x=﹣1,分别与x轴交于点A,B(A在B的左侧),与y轴交于点C.
(1)求b的值;
(2)若将线段BC绕点C顺时针旋转90°得到线段CD,问:点D在该抛物线上吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
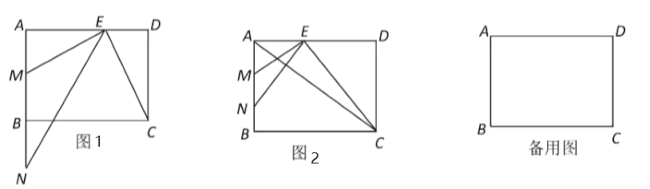
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在射线
在射线![]() 上,且
上,且![]() 是
是![]() 和
和![]() 的比例中项.
的比例中项.
(1)如图1,求证:![]() ;
;
(2)如图2,当点![]() 在线段
在线段![]() 之间,联结
之间,联结![]() ,且
,且![]() 与
与![]() 互相垂直,求
互相垂直,求![]() 的长;
的长;
(3)联结![]() ,如果
,如果![]() 与以点
与以点![]() 、
、![]() 、
、![]() 为顶点所组成的三角形相似,求
为顶点所组成的三角形相似,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个8cm×16cm智屏手机抽象成一个矩形ABCD,其中AB=8cm,AD=16cm,现将正在竖屏看视频的这个手机围绕它的中心R顺时针旋转90°后改为横屏看视频,其中,M是CD的中点,则图中等于45°的角有_____个.(按图中所标字母写出符合条件的角)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个边长为60米的正六边形跑道,P、Q两人同时从A处开始沿相反方向都跑一圈后停止,P以4米/秒逆时针方向、Q以5米/秒顺时针方向,PQ的距离为d米,设跑步时间为x秒,令d2=y,
(1)跑道全长为 米,经过 秒两人第一次相遇.
(2)当P在BC上,Q在EF上时,求y关于x的函数解析式;并求相遇前当x为多少时,他们之间的距离最大.
(3)直接写出P、Q在整个运动过程中距离最大时的x的值及最大的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣![]() x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.
x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.

(1)求该抛物线的解析式;
(2)当△PDE是以DE为底边的等腰三角形时,求点P的坐标;
(3)当四边形ACPB的面积最大时,求点P的坐标并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
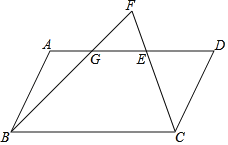
【题目】如图,在ABCD中,点E是边AD上一点,延长CE到点F,使∠FBC=∠DCE,且FB与AD相交于点G.
(1)求证:∠D=∠F;
(2)用直尺和圆规在边AD上作出一点P,使△BPC∽△CDP,并加以证明.(作图要求:保留痕迹,不写作法.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
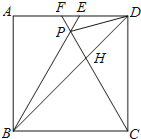
【题目】如图,在正方形![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() 、
、![]() 的延长线分别交
的延长线分别交![]() 于点
于点![]() 、
、![]() ,连结
,连结![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .给出下列结论:①
.给出下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 其中正确结论的序号是( )
其中正确结论的序号是( )
A.①②B.②③④C.①③④D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com