

分析 (1)方法一、求出正方形的边长,再根据正方形面积公式求出即可;
方法二、根据大正方形面积减去4个矩形面积,即可得出答案;
(2)根据(1)阴影部分的面积相等,即可得出等式;
(3)①把a-b=5两边平方,利用完全平分公式,即可解答;
②根据(a+b)2=(a-b)2+4ab,即可解答;
③利用完全平分公式,即可解答.
解答 解:(1)阴影部分是正方形,正方形的边长是m-n,即阴影部分的面积是(m-n)2,
又∵阴影部分的面积S=(m+n)2-4mn,
故答案为:(m-n)2,(m+n)2-4mn.
(2)(a-b)2=(a+b)2-4ab,
故答案为:(a-b)2=(a+b)2-4ab.
(3)①∵a-b=5,ab=-6,
∴(a-b)2=52
∴a2-2ab+b2=25,
a2+b2=25+2ab=25-12=13,
故答案为:13.
②(a+b)2=(a-b)2+4ab=52-4×(-6)=49.
故答案为:49.
③${x}^{4}+\frac{1}{{x}^{4}}$
=$({x}^{2}+\frac{1}{{x}^{2}})^{2}-2$
=$[(x+\frac{1}{x})^{2}-2]^{2}-2$
=(32-2)2-2
=47.
点评 本题主要考查完全平分公式,如何准确地确定三个代数式之间的等量关系是解题的关键.


科目:初中数学 来源: 题型:解答题
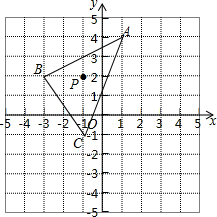 如图,△ABC的三个顶点坐标分别A(1,4),B(-3,2),C(-1,-1),点P(x0,y0)为△ABC中的任意一点,经平移后点P的对应点为P1(x0+3,y0-2),将△ABC作同样的平移得到△A1B1C1
如图,△ABC的三个顶点坐标分别A(1,4),B(-3,2),C(-1,-1),点P(x0,y0)为△ABC中的任意一点,经平移后点P的对应点为P1(x0+3,y0-2),将△ABC作同样的平移得到△A1B1C1查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com