
 如图,点E,F为正方形ABCD边BC,CD上的点,且△CEF的周长等于正方形ABCD周长的一半.
如图,点E,F为正方形ABCD边BC,CD上的点,且△CEF的周长等于正方形ABCD周长的一半.分析 (1)先把△ADF绕着点A按顺时针方向旋转90°后,得到△ABG,得出点G、B、E在一条直线上,GE=BE+BG=BE+DF,再根据△CEF的周长等于正方形ABCD周长的一半,得出EF=DF+BE,进而得到EF=EG,再判定△EAF≌△EAG(SSS),即可得到∠EAF=∠EAG=$\frac{1}{2}$∠GAF=45°;
(2)根据△EAF≌△EAG,且AB⊥GE,AM⊥EF,即可得到△EAF的面积=△EAG的面积,即$\frac{1}{2}$×GE×AB=$\frac{1}{2}$×EF×AM,再根据EF=EG(已证),得到AB=AM,最后运用等量代换,即可得到AM=AD.
解答  解:(1)把△ADF绕着点A按顺时针方向旋转90°后,得到△ABG,
解:(1)把△ADF绕着点A按顺时针方向旋转90°后,得到△ABG,
∴AF=AG,BG=DF,∠ABG=∠D=90°,∠GAF=90°,
又∵正方形ABCD中,∠ABC=90°,
∴点G、B、E在一条直线上,
∴GE=BE+BG=BE+DF,①
∵△CEF的周长等于正方形ABCD周长的一半,
∴EF+EC+FC=DC+BC=DF+FC+EC+BE,
即EF=DF+BE,②
由①②可得,EF=EG,
在△EAF和△EAG中,
$\left\{\begin{array}{l}{AF=AG}\\{EF=EG}\\{AE=AE}\end{array}\right.$,
∴△EAF≌△EAG(SSS),
∴∠EAF=∠EAG,
∴∠EAF=$\frac{1}{2}$∠GAF=45°;
(2)证明:∵△EAF≌△EAG,且AB⊥GE,AM⊥EF,
∴△EAF的面积=△EAG的面积,
即$\frac{1}{2}$×GE×AB=$\frac{1}{2}$×EF×AM,
又∵EF=EG(已证),
∴AB=AM,
又∵正方形ABCD中,AB=AD,
∴AM=AD.
点评 本题主要考查了正方形的性质以及全等三角形的判定与性质的综合应用,解决问题的关键是运用旋转变换进行解答.解第(2)题时注意运用:全等三角形对应边上的高相等.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
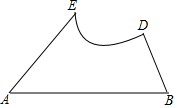 有一个三角形工件△ABC,根据安装需要,把∠C切掉了,如图,现在要在工件上画出一条线段,使它是∠C的平分线在阴影面留下的那部分.
有一个三角形工件△ABC,根据安装需要,把∠C切掉了,如图,现在要在工件上画出一条线段,使它是∠C的平分线在阴影面留下的那部分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | xy | B. | 100x+y | C. | 10x+y | D. | x+y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com