
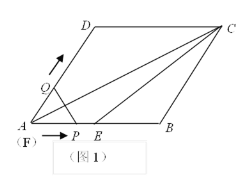
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦ1Θ§Νβ–ΈABCDΒΡ±Ώ≥ΛΈΣ6Θ§ΓœDAB=60ΓψΘ§ΒψE «ABΒΡ÷–ΒψΘ§Ν§Ϋ”ACΓΔECΘ°ΒψQ¥”ΒψA≥ωΖΔΘ§―Ί’έœΏAΓΣDΓΣC‘ΥΕ·Θ§Ά§ ±ΒψP¥”ΒψA≥ωΖΔΘ§―Ί…δœΏAB‘ΥΕ·Θ§PΓΔQΒΡΥΌΕ»ΨυΈΣΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΘΜ“‘PQΈΣ±Ώ‘ΎPQΒΡΉσ≤ύΉςΒ»±ΏΓςPQFΘ§ΓςPQF”κΓςAEC÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§Β±ΒψQ‘ΥΕ·ΒΫΒψC ±PΓΔQΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ§…η‘ΥΕ·ΒΡ ±ΦδΈΣtΘ°
Θ®1Θ©Β±Β»±ΏΓςPQFΒΡ±ΏPQ«ΓΚΟΨ≠ΙΐΒψD ±Θ§«σ‘ΥΕ· ±ΦδtΒΡ÷ΒΘΜΒ±Β»±ΏΓςPQFΒΡ±ΏQF«ΓΚΟΨ≠ΙΐΒψE ±Θ§«σ‘ΥΕ· ±ΦδtΒΡ÷ΒΘΜ
Θ®2Θ©‘Ύ’ϊΗω‘ΥΕ·Ιΐ≥Χ÷–Θ§«κ«σ≥ωS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΚΆœύ”ΠΒΡΉ‘±δΝΩtΒΡ»Γ÷ΒΖΕΈßΘΜ
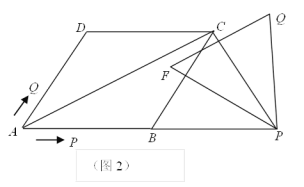
Θ®3Θ©»γΆΦ2Θ§Β±ΒψQΒΫ¥οCΒψ ±Θ§ΫΪΒ»±ΏΓςPQF»ΤΒψP–ΐΉΣΠΝ Γψ (0<ΠΝ<360Γψ)Θ§÷±œΏPF Ζ÷±π”κ÷±œΏACΓΔ÷±œΏCDΫΜ”ΎΒψMΓΔNΘ° «Ζώ¥φ‘Ύ’β―υΒΡΠΝ Θ§ ΙΓςCMNΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ω¥Υ ±œΏΕΈCMΒΡ≥ΛΕ»ΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ;Θ®2Θ©ΦϊΫβΈω;Θ®3Θ©ΦϊΫβΈω.
;Θ®2Θ©ΦϊΫβΈω;Θ®3Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“β«σ≥ω‘ΥΕ·ΒΡΨύάκΘ§‘Ό≥ΐ“‘ΥΌΕ»Φ¥Ω…«σ≥ω ±ΦδΘΜ
Θ®2Θ©Ζ÷Β±0ΘΦtΓή3 ±Θ§Β±3ΘΦtΓή6 ±Θ§Β±6ΘΦtΓή9 ±Θ§Β±9ΘΦtΓή12 ±Θ§ΥΡ÷÷«ιΩωΘ§Ζ÷±π«σ≥ω÷ΊΒΰ≤ΩΖ÷ΟφΜΐΦ¥Ω…ΘΜ
Θ®3Θ©Ζ÷ΫΜΒψΕΦ‘ΎBCΉσ≤ύΘ§ΕΞΫ«ΈΣ120ΓψΘ§ΫΜΒψΕΦ‘ΎBC”“≤ύ ±Θ§ΕΞΫ«Ω…ΡήΈΣ30ΓψΚΆ120ΓψΘΜΫΜΒψ‘ΎBCΝΫ≤ύ ±Θ§ΕΞΫ«ΈΣ150ΓψΫχ––Χ÷¬έ«σΫβΦ¥Ω….
ΫβΘΚΘ®1Θ©Β±Β»±ΏΓςPQFΒΡ±ΏPQ«ΓΚΟΨ≠ΙΐΒψD ±Θ§
»γΆΦ1,
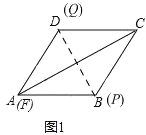
AQ=AD=6Θ§
Γύt=6Γ¬1=6Θ®ΟκΘ©ΘΜ
Β±Β»±ΏΓςPQFΒΡ±ΏQF«ΓΚΟΨ≠ΙΐΒψE ±Θ§
»γΆΦ2,

”…Νβ–ΈABCDΒΡ±Ώ≥ΛΈΣ6Θ§ΓœDAB=60ΓψΘ§PΓΔQΒΡΥΌΕ»ΨυΈΣΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»Θ§
÷ΣΘΚΓœAPQ=60ΓψΘ§ΓœQEB=60ΓψΘ§
ΓύQEΓΈADΘ§
ΓΏΒψE «ABΒΡ÷–ΒψΘ§
Γύ¥Υ ±ΒψQ «CDΒΡ÷–ΒψΘ§
Ω…«σΘΚAD+DQ=6+3=9Θ§
Υυ“‘t=9Γ¬1=9Θ®ΟκΘ©ΘΜ
Θ®2Θ©»γΆΦ3,
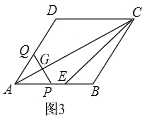
Β±0ΘΦtΓή3 ±Θ§
”…Νβ–ΈABCDΒΡ±Ώ≥ΛΈΣ6Θ§ΓœDAB=60ΓψΘ§
Ω…«σΘΚΓœPAG=30ΓψΘ§
ΓΏΓœAPQ=60ΓψΘ§
ΓύΓœAGP=90ΓψΘ§
”…AP=tΘ§Ω…«σΘΚPG=![]() tΘ§AG=
tȧAG=![]() tȧ
tȧ
ΓύS=![]() PGΓΝAG=
PGΓΝAG=![]() t2ΘΜ
t2ΘΜ
Β±3ΘΦtΓή6 ±Θ§
»γΆΦ4,
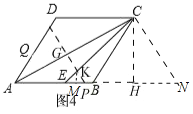 ,
,
AE=3ȧAP=tȧ
ΓύPE=t-3Θ§
ΙΐΒψCΉςABΒΡ¥ΙœΏΘ§¥ΙΉψΈΣHΘ§
”…Νβ–ΈABCDΒΡ±Ώ≥ΛΈΣ6Θ§ΓœDAB=60ΓψΘ§
Ω…«σΘΚCH=3![]() Θ§BH=3Θ§EH=6Θ§
Θ§BH=3Θ§EH=6Θ§
tanΓœKEB=![]() Θ§
Θ§
ΙΐΒψKΉςKMΓΆABΘ§ΉςCNΓΈPKΫΜABΒΡ―”≥ΛœΏ”ΎNΘ§
ΓΏΓςEKPΓΉΓςECNΘ§Ω…ΒΟ
![]() =
=![]() Θ§
Θ§
Ω…«σKM=![]() Θ§
Θ§
ΓύSΓςPEK=![]() Θ§
Θ§
Ω…«σΓœQAG=30ΓψΘ§
”÷ΓœAQG=60ΓψΘ§AQ=tΘ§
Ω…«σΓœAGQ=90ΓψΘ§
DG=![]() tȧGQ=
tȧGQ=![]() tȧ
tȧ
ΓύSΓςAGQ=![]() t2Θ§
t2Θ§
Β»±Ώ»ΐΫ«–ΈAPDΒΡΟφΜΐΈΣΘΚ![]() Θ§
Θ§
ΓύS=![]() -
-![]() t2-
t2-![]() =
=![]() +
+![]() t
t![]() Θ§
Θ§
Β±6ΘΦtΓή9 ±Θ§
»γΆΦ5Θ§
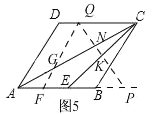 Θ§
Θ§
”κ«ΑΆ§άμΩ…«σΘΚSΓςFQP=9![]() Θ§
Θ§
SΓςGQN=![]() Θ§
Θ§
SΓςKEP=![]() Θ§
Θ§
ΓύS=9![]() -
-![]() -
-![]() =
=![]() t2+4
t2+4![]() t
t![]() Θ§
Θ§
Β±9ΘΦtΓή12 ±Θ§
»γΆΦ6Θ§
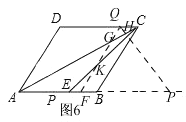
«σ≥ωΘΚSΓςPQF=9![]() Θ§
Θ§
SΓςQGH=![]() Θ§
Θ§
SΓςNEP=![]() Θ§
Θ§
SΓςKEF=![]() Θ§
Θ§
ΓύS=SΓςPQF-SΓςQGH-SΓςNEP+SΓςKEF=9![]() -
-![]() -
- ![]() +
+![]() =
=![]() t25
t25![]() t+30
t+30![]() ΘΜ
ΘΜ
Θ®3Θ©Ρφ ±’κ–ΐΉΣΘΚ
ΔΌΠΝ=150ΓψΘ§»γΆΦ7Θ§
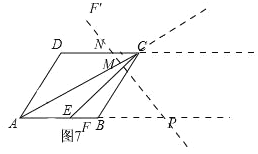
¥Υ ±Θ§“Ή«σΓœCNM=ΓœNCM=ΓœAPM=ΓœMAP=ΓœDAP=30ΓψΘ§
Ω…÷ΛΓςACDΓΉΓςAPMΘ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
“Ή«σAP=12Θ§AC=6![]() Θ§AD=6Θ§
Θ§AD=6Θ§
ΫβΒΟΘΚAM=4![]() Θ§
Θ§
Υυ“‘Θ§CM=2![]() ΘΜ
ΘΜ
ΔΎΠΝ=105ΓψΘ§»γΆΦ8,
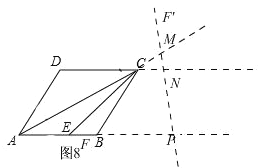
¥Υ ±Θ§“Ή«σCM=CNΘ§ΓœCMN=ΓœCNM=ΓœAPM=75ΓψΘ§
ΓύAM=AP=12Θ§
‘ΎΝβ–ΈABCD÷–Θ§AD=CD=6Θ§ΓœD=120ΓψΘ§
Ω…«σAC=6![]() Θ§
Θ§
Υυ“‘Θ§CM=12=6![]() ΘΜ
ΘΜ
ΔέΠΝ=60ΓψΘ§»γΆΦ9,
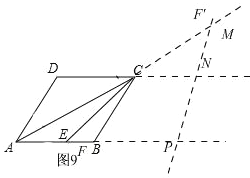
¥Υ ±Θ§“Ή«σΓœCMN=ΓœMCN=ΓœACB=30ΓψΘ§
ΓύBCΓΈPMΘ§
”…AB=BP=6Ω…ΒΟΘ§CM=AC=6![]() ,
,
Υυ“‘ΘΚCM=6![]() ΘΜ
ΘΜ
ΔήΠΝ=15ΓψΘ§»γΆΦ10,
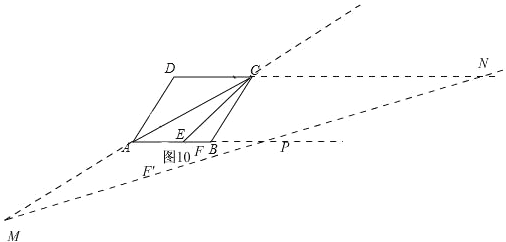
¥Υ ±Θ§“Ή«σΓœAPM=ΓœM=15ΓψΘ§
ΓύAM=AP=12Θ§
Υυ“‘ΘΚCM=AM+ACΘ§
CM=12+6![]() Θ°
Θ°


 Κ°ΦΌ¥¥–¬–ΆΉ‘÷ς―ßœΑΒΎ»ΐ―ßΤΎΚ°ΦΌœΈΫ”œΒΝ–¥πΑΗ
Κ°ΦΌ¥¥–¬–ΆΉ‘÷ς―ßœΑΒΎ»ΐ―ßΤΎΚ°ΦΌœΈΫ”œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ»γΆΦΘ§’ΐΖΫ–ΈABCD÷–Θ§AD=4Θ§ΒψE‘ΎCD…œΘ§DE=3CEΘ§F «AD…œ“λ”ΎDΒΡΒψΘ§«“ΓœEFB=ΓœFBCΘ§‘ρtanΓœDFE=Θ® Θ©

A. 2![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ”…±Ώ≥ΛΈΣ1ΗωΒΞΈΜ≥ΛΕ»ΒΡ–Γ’ΐΖΫ–ΈΉι≥…ΒΡΆχΗώΆΦ÷–”–ΗώΒψΓςABCΘ°
Θ®ΉΔΘΚΕΞΒψ‘ΎΆχΗώœΏΫΜΒψ¥ΠΒΡ»ΐΫ«–ΈΫ–ΉωΗώΒψ»ΐΫ«–ΈΘ©
Θ®1Θ©ΆΦ÷–ABΒΡ≥ΛΈΣ_________ΗωΒΞΈΜ≥ΛΕ»ΘΜ
Θ®2Θ©÷Μ”ΟΟΜ”–ΩΧΕ»ΒΡ÷±≥ΏΘ§Α¥»γœ¬“Σ«σΜ≠ΆΦΘΚ
ΔΌ “‘ΒψCΈΣΈΜΥΤ÷––ΡΘ§ΉςΓςDECΓΉΓςABCΘ§«“œύΥΤ±»ΈΣ1ΓΟ2ΘΜ
ΔΎ»τΒψBΈΣ‘≠ΒψΘ§ΒψAΘ®1Θ§3Θ©Θ§«κ‘ΎΆΦ2÷–Μ≠≥ωΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§÷±Ϋ”≥ωΓςABCΒΡΆβ–ΡΒΡΉχ±ξ______________

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ![]() ÷–Θ§
÷–Θ§![]() Θ°
Θ°
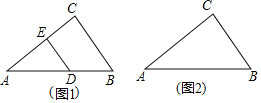
![]() »γΆΦ1Θ§»τ
»γΆΦ1Θ§»τ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§«“
Θ§«“![]() Θ§«σADΒΡ≥ΛΘΜ
Θ§«σADΒΡ≥ΛΘΜ
![]() »γΆΦ2Θ§«κάϊ”ΟΟΜ”–ΩΧΕ»ΒΡ÷±≥ΏΚΆ‘≤ΙφΘ§‘ΎœΏΕΈAB…œ’““ΜΒψFΘ§ ΙΒΟΒψFΒΫ±ΏACΒΡΨύάκΒ»”Ύ
»γΆΦ2Θ§«κάϊ”ΟΟΜ”–ΩΧΕ»ΒΡ÷±≥ΏΚΆ‘≤ΙφΘ§‘ΎœΏΕΈAB…œ’““ΜΒψFΘ§ ΙΒΟΒψFΒΫ±ΏACΒΡΨύάκΒ»”Ύ![]() ΉΔΘΚ≤Μ–¥ΉςΖ®Θ§±ΘΝτΉςΆΦΚέΦΘΘ§Ε‘ΆΦ÷–…φΦΑΒΫΒΡΒψ”ΟΉ÷ΡΗΫχ––±ξΉΔ
ΉΔΘΚ≤Μ–¥ΉςΖ®Θ§±ΘΝτΉςΆΦΚέΦΘΘ§Ε‘ΆΦ÷–…φΦΑΒΫΒΡΒψ”ΟΉ÷ΡΗΫχ––±ξΉΔ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
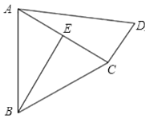
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡ±Ώ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ”Ύ
”Ύ![]() Θ§
Θ§
Θ®1Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() Θ§
Θ§![]() Θ§«σΥΡ±Ώ–Έ
Θ§«σΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΘ°
ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
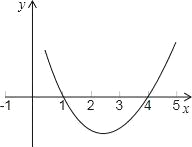
ΓΨΧβΡΩΓΩ“―÷ΣΘ§Εΰ¥ΈΚ· ΐy=ax2©¹5x+cΒΡΆΦœσ»γΆΦΘ°
(1)«σ’βΗωΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΚΆΥϋΒΡΆΦœσΒΡΕΞΒψΉχ±ξΘΜ
(2)Ιέ≤λΆΦœσΘ§ΜΊ¥πΘΚΚΈ ±yΥφxΒΡ‘ω¥σΕχ‘ω¥σΘΜΚΈ ±yΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
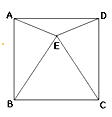
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCDΡΎΒΡΓςBECΈΣ’ΐ»ΐΫ«–ΈΘ§«σΓœDEAΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®±ΨΧβΙ≤10Ζ÷Θ©Υ°Ιϊ≈ζΖΔ –≥Γ”–“Μ÷÷ΗΏΒΒΥ°Ιϊ,»γΙϊΟΩ«ßΩΥ”·άϊΘ®ΟΪάϊ»σΘ©10‘Σ,ΟΩΧλΩ… έ≥ω500«ßΩΥΘ°Ψ≠ –≥ΓΒς≤ιΖΔœ÷,‘ΎΫχΜθΦέ≤Μ±δΒΡ«ιΩωœ¬,»τΟΩ«ßΩΥ’«Φέ1‘Σ,»’œζΝΩΫΪΦθ…Ό20«ßΩΥΘ°
Θ®1Θ©»τ“‘ΟΩ«ßΩΥΡή”·άϊ18‘ΣΒΡΒΞΦέ≥ω έ,Έ ΟΩΧλΒΡΉήΟΪάϊ»σΈΣΕύ…Ό‘Σ?
Θ®2Θ©œ÷ –≥Γ“Σ±Θ÷ΛΟΩΧλΉήΟΪάϊ»σ6000‘Σ,Ά§ ±”÷“Σ ΙΙΥΩΆΒΟΒΫ ΒΜί,‘ρΟΩ«ßΩΥ”Π’«ΦέΕύ…Ό‘Σ?
Θ®3Θ©œ÷–ηΑ¥ΟΪάϊ»σΒΡ10%ΫΜΡ…Ης÷÷ΥΑΖ―,»ΥΙΛΖ―ΟΩ»’Α¥œζ έΝΩΟΩ«ßΩΥ÷ß≥ω0Θ°9‘Σ,Υ°ΒγΖΩΉβΖ―ΟΩ»’102‘Σ,»τ Θœ¬ΒΡΟΩΧλΉή¥Ωάϊ»σ“Σ¥οΒΫ5100‘Σ,‘ρΟΩ«ßΩΥ’«Φέ”ΠΈΣΕύ…Ό?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com